Aloin miettiä auton kulutusta. Sähköautoissa ilmoitetaan kWh sataa kilometriä kohden, mikä vaikuttaa järkevältä. Tämänhän tarkoittaa energian yksiköitä pituusyksikköä kohti. Mutta entä polttoainetta käyttävät autot: mitä oikeasti tarkoittaakaan kulutus litroina sadalla kilometrillä. Litrat voidaan ilmoittaa kuutiometreinä, joten auton kulutus voidaan ilmoittaa neliömetreinä. Mitä se oikein tarkoittaa?

Hauska kysymys. Jos auton kulutus on vaikka $5\; l/100\; km$, niin se on sama kuin

eli $0{,}05\; mm^2$. Auton kulutus tosiaan voidaan ilmoittaa pinta-alana, jonka suuruusluokka on neliömillimetrin murto-osa.

 Niin, mutta mitä se tarkoittaa?

 Kulutus voidaan tulkita siten, että se kertoo auton jälkeensä jättämän kuvitteellisen polttoainevanan pinta-alan (Kuva 1).

Kuva 1. Polttoaineen kulutus kertoo polttoainevanan pinta-alan.

Ahaa, niinpä tietenkin.

Usein fysiikan opetuksessa kannustetaan käyttämään suoraviivaisia SI-yksiköitä, koska ne ovat virallisia ja siten ensimmäinen ehdokas suureiden yksiköiksi. Joskus suoraviivaisin yksikkö ei kuitenkaan ole se havainnollisin. Kulutuslukemaa $0{,}05\; mm^2$ on vaikea mieltää arjessa merkitykselliseksi. Paljon käytännöllisempää on ilmoittaa kulutus litroina satoja kilometrejä kohden, sillä se auttaa hahmottamaan paljonko tankissa on oltava polttoainetta tehtävää matkaa varten.

Kulutuksen pohtiminen tuo esiin myös yleisemmän huomion: yksiköillä on aina täsmällinen merkitys. Yksiköt ovat fysiikassa keskeisessä asemassa ja niiden hallitsemisesta on paljon hyötyä myös arkisissa tilanteissa.

Jos esimerkiksi haluamme laskea tietyn matkan kustannukset, niin voimme kertoa polttoaineen hinnan $P$ (€/L), kulutuksen $K$ (L/100 km) ja matkan $M$ (km), eli

 Mutta tämä kaavahan ravisteltiin hihasta, joten mistä tiedämme, että tämä matemaattinen kaava myös on oikein? Yksikkötarkastelulla. Kaavassa suureiden yksiköt kerrotaan myös keskenään, jolloin litrat ja kilometrit supistuvat pois

ja kustannuksen yksiköksi saadaan €, kuten kuuluukin.

Mutta eihän € ole fysiikan yksikkö.

Euro ei ehkä liity luonnonilmiöön, mutta sillä ei ole väliä. Kaikki suureet ilmoitetaan lukuarvon ja suuretta vastaavan yksikön avulla. Ja kaikki yksiköt toimivat kaavoissa kuten mikä tahansa symbolit, riippumatta yksikköä vastaavan suureen luonteesta.

Tässä yhteydessä on hyvä korostaa myös dimension ja yksikön eroa. Litra, kuutiometri, gallona ja ruokalusikka ovat kaikki yksiköitä, jotka liittyvät tilavuuden dimensioon. Dimensio kertoo suureen luonteen (“mistä on kyse”); yksikkö puolestaan antaa lukuarvolle yhteisesti sovitun mittatikun. Pelkällä dimensiolla on vaikea ilmaista mitään määrällisesti. Esimerkiksi ilmaisu “maitoa on kolme ja puoli tilavuutta” olisi merkityksetön; mittatikku määrälle puuttuu. “Maitoa on kolme ja puoli litraa” on fysikaalisesti mielekäs ilmaisu.

Eli esimerkiksi “energia” on dimensio ja joule ja kWh sen yksiköitä. Mutta miksi sähkön yhteydessä energia ilmoitetaan nimenomaan kilowattitunteina, vaikka SI-yksikkö on joule?

Tässä pätee sama näkökulma käytännöllisyydestä kuin polttoaineenkulutuksessa. Jos pyykkikoneen yhden pesun energiankulutukseksi ilmoitetaan $3{,}4$ MJ, sen merkitystä arjen toiminnassa on vaikea hahmottaa. Energiankulutus $0{,}95$ kWh on näppärämpi hahmottaa: energiaa kulutetaan vaikka tunnin ajan noin kilowatin teholla tai puolen tunnin ajan parin kilowatin teholla. Watti on SI-yksikkö ja tunti on arjessa hahmotettava aikaskaala, joten kWh on toimiva yhdistelmä. Tämä energiankulutuksen yksikkö on luonnollisesti siirtynyt myös sähköautoihin, mihin viittasit alun kysymyksessäsi. SI-yksikköjärjestelmä on tarpeellinen ja muodostaa yksiköille vankan perustan. Arjessa käytettävät suureiden yksiköt on kuitenkin aina vapaasti valittavissa; siksi ne kannattaa valita mahdollisimman havainnollisiksi ja merkityksellisiksi. 

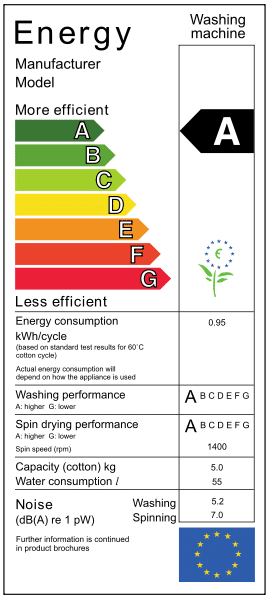
Kuva 2. Energiatodistus pyykkikoneelle, joka kuluttaa keskimäärin $0{,}95$ kWh energiaa koneellista kohden.

Erilaiset yksiköt kuitenkin joskus hämmentävät.

Niinpä. Jos itse on tottunut ilmaisemaan suureen arjessa merkityksellisen yksikön avulla, niin uuteen yksikköön siirtyminen on vaikeaa. Esimerkiksi aiemmin verenpaine mitattiin laitteella, joka hyödynsi paineen mittaamista elohopeapatsaan avulla (Kuva 3). Näin paine oli luontevaa ilmaista elohopeamillimetreinä (mmHg eli hydrostaattinen paine, jonka mitatun korkuinen nestemäinen elohopeapatsas aiheuttaa painovoiman vaikutuksesta). Nykyään verenpainetta mitataan sähköisillä paineantureilla, mutta mmHg on jäänyt verenpaineen mittayksiköksi historiallisista syistä, ainakin toistaiseksi.

Kuva 3. Elohopeaverenpainemittari.

Erilaisten mittayksiköiden hämmennykset hälventämiseksi tarpeellista on yksikkömuunnosten hallitseminen. Muunnoksissa kannattaa muistaa aiemmin mainitsemani yksiköiden luonne: ne käyttäytyvät matemaattisissa kaavoissa kuten mitkä tahansa symbolit.

Esimerkiksi $h=3600 \;s$ ja siten 

Tai nopeus 30 jalkaa sekunnissa on kilometreinä tunnissa

Ainoa yksikkö, joka käyttäytyy hieman muista poiketen on radiaani. Kaavoissa yksikkö “rad” nimittäin käyttäytyy aivan kuten sitä ei olisikaan; yksikköä pidetään mukana lausekkeissa vain ikään kuin muistuttamaan, että kyseessä on kulmasuure.

Ja kuten kysymyksessä pakkasen hyytävyydestä (osio: "Miten tuulen hyytävyys määräytyy?") keskustelimme, lausekkeisiin tulee suhtautua erityisen valppaasti ja jopa epäilevästi, mikäli niissä “suure x tulee esittää yksikössä y”. Tällöin lausekkeiden laatija ei ole suhtautunut yksiköihin niiden ansaitsemalla arvokkuudella ja huolellisuudella.

Yksiköitä vastaavien dimensioiden tarkastelusta voi olla hyötyä arjessa myös muilla tavoin. Tällaisen dimensioanalyysin avulla fysiikan lausekkeita voidaan jopa loihtia lähes tyhjästä. Esimerkiksi, muistatko miten vaikkapa heilurikellon heilurin heilahdusaika riippuu heilurin ominaisuuksista?

Ööö — no en nyt tähän hätään muista.

En minäkään, mutta pohditaanpa. Mitkä asiat vaikuttavat heilahdusaikaan?

Kuva 4. Heilurikellon kulkunopeus perustuu heilurin värähtelyjaksoon.

No, heilurin pituus… heilurin massa ja…

Eli pituus ja massa, hyvä. Palautuminen heilurin tasapainoasemaan tapahtuu painovoiman vaikutuksesta, joten yksi suure on painovoima. Mikäli ilmanvastus ja kitka jätetään huomiotta, niin muita asioita heilahdusaikaan ei sitten vaikutakaan. Eli heilahdusaika $T$ määräytyy jotenkin heilurin pituudesta $L$, heilurin massasta $m$ ja painovoimasta, jota kuvataan putouskiihtyvyydellä $g=9{,}81\; m/s^2$. Aika $T$ voidaan ilmaista sekunneissa, pituus $L$ metreinä, massa $m$ kilogrammoina ja $g$ metreinä per sekunti per sekunti eli $m/s^2$. Siten heilahdusaika on siis jokin, tuntematon $L$:n, $m$:n ja $g$:n funktio

Yksiköiden konsistenttiuden eli niin kutsutun dimensionaalisen homogeenisuuden vuoksi kuitenkin tiedämme, että funktion $f$ yksikön täytyy olla sekunti! (Tai yleisemmin, funktion dimension täytyy kuvata ajan dimensiota.) Funktion siis täytyy olla sellainen, että kolmesta suureesta muodostuu sekunnin yksikkö ja ajan dimensio. Huomaamme, että kilogramman yksikköä ei ole missään muussa suureessa kuin $m$:ssä. Jos siis funktiossa ilmenee suure $m$, niin kilogramman yksikköä ei mitenkään saa hävitettyä $L$:n ja $g$:n avulla. $T$:ssä kilogrammaa ei ole mukana, joten funktio ei voi riippua $m$:stä lainkaan!

Oho! Mutta eikö painovoima nyt kuitenkin vaikuta voimakkaammin painavampaan punnukseen?

Heilahdusajan voi laskea myös liikeyhtälön avulla, mutta tulos on sama: se ei riipu heilurin massasta. Liikeyhtälön avulla voimme ymmärtää syyn: painavampi punnus myös kiihtyy hitaammin, mikä täsmälleen kumoaa voimakkaamman painovoiman vaikutuksen. Dimensioanalyysi ei kerro syytä, mutta antaa oikean tuloksen. Dimensioanalyysiä tehdessä tulee toisaalta olla erittäin huolellinen mukaan otettavien suureiden suhteen. Jos jokin keskeinen suure unohtuu, analyysi on tuomittu epäonnistumaan. Jos suureita puolestaan tulee liikaa, analyysi saattaa tulla vaikeaksi. Onneksi esimerkissämme heilurin massa $m$ osoittautui ylimääräiseksi melko helposti.

Jatketaan. Saimme siis heilurin ajalle lausekkeen

Koska $L$:n yksikkö on $m$ ja $g$:n yksikkö on $m/s^2$, niin ainoa mahdollinen tapa muodostaa näistä yksiköistä sekunnin yksikkö on operaatio $\sqrt{L/g}$. Siten

Ja voilá! Siinä on lauseke heilurin jaksonajalle. 

Mutta mikä on tuo vakio?

Vakiota ei pysty saamaan pelkän dimensioanalyysin avulla, siihen tarvittaisiin liikeyhtälöiden ratkaisua, jotka antavat $\text{vakio}=2\pi$. Tällaista vakiota kutsutaan usein geometriseksi vakioksi. Mutta huomaa, että yllä oleva lauseke syntyi puhtaasti dimensioanalyysin avulla, käyttämättä yhtäkään fysiikan periaattetta! Lähes taikutta!

Kun tiedämme, että $T\propto \sqrt{L}$, voimme jo esimerkiksi päätellä että kellon heiluria tulisi lyhentää $0{,}14$%, mikäli kello jätättää minuutin vuorokaudessa. Eli dimensioanalyysistä olisi jo riittävä apu tilanteeseen, jossa kellon käyntinopeutta pitäisi muuttaa. 

Dimensioanalyysin työkalut ovat tietyillä fysiikan aloilla jopa elinehto. Esimerkiksi virtausdynamiikan ongelmat ovat usein niin vaikeita, että niitä ei voi ratkaista analyyttisesti lainkaan. Virtausdynamiikan Navier-Stokesin yhtälö on eräs niin kutsutuista millennium-ongelmista. Voimme kuitenkin tutkia nesteiden ja kaasujen virtauksia pienoismalleissa ja skaalata pienoismallien kokemia voimia ja oikean kokoisiin laivoihin ja lentokoneisiin nimenomaan dimensioanalyysin tulosten avulla.

Eräässä toisessa kysymyksessä (osio: "Miksi taivas on sininen ja iltarusko punainen?") perustelemme dimensioanalyysin avulla jopa sen miksi taivas on sininen!

Oho! Mutta nyt menimme melko kauaksi alkuperäisestä kysymyksestä auton kulutuksesta.

No joo, pahoittelen. Mutta dimensioiden ja yksiköiden hallitseminen — liittyivät ne sitten suoraan luonnonilmiöihin tai eivät — on arvokas lisä arjen suureviidakossa seikkailemiseen.

Otetaan tähän loppuun vielä melko pitkälle menevä esimerkki siitä, miten dimensioanalyysia voidaan käyttää kinkun paistoajan määrittämiseen. Jospa se inspiroisi tekemään dimensioanalyysia jollekin itsellesi relevanttiin arjen tilanteeseen.

Video 1. Dimensioanalyysi siitä miten kinkun paistoaika riippuu kinkun painosta.

Tuli vielä mieleen, että mikä yksikkö sitten olikaan kuutioeekkeri? Roope Ankan rahasäiliön tilavuushan on kolme kuutioeekkeriä.

Kuutioeekkeri yksikkönä on kyllä järkevä. Eekkeri on pinta-alan yksikkö ja se kuutioituna on pituuden yksikkö kuudenteen potenssiin: eekkeri$^3$=$66{,}3\times 10^9\; m^6$. Ankuankkamaisesti se tosin on fysikaalisesti merkityksetön.