Tässä taannoin uutisissa ennustettiin nollakeliä, mutta navakan pohjoistuulen vuoksi varoitettiin hyytävästä ilmasta tuulen vuoksi. Jäin miettimään, että mistä tuulen hyytävyyden “tuntuu kuin” -lämpöasteet saadaan?

Kuva 1: Pakkanen puree tuulella.

Tutkitaanpa asiaa hieman. Wikipedian mukaan tuulen hyytävyys eli pakkasen purevuus saadaan kaavasta

$T_h=13{,}12+0{,}6215\times T_{ilma} - 13{,}956\times v^{0{,}16} + 0{,}4867\times T_{ilma}\times v^{0{,}16}$,

missä $T_{ilma}$ on ilman lämpötila ja $v$ on tuulen nopeus metreinä sekunnissa, kymmenen metrin korkeudessa. Tuulen nopeuden kasvojen korkeudella arvioidaan eräänlaisella nyrkkisäännöllä kertomalla tämä nopeus tekijällä $2 / 3$. Tällä kaavalla voimme laatia taulukon, joita silloin tällöin näkee esitettävän mediassa (Kuva 2). Esimerkiksi $-20^\circ C$ ilman lämpötilalla ja $10\; m/s$ tuulen nopeudella ilma tuntuu yhtä kylmältä kuin jos täysin tyvenessä olisi $-34^\circ C$ astetta pakkasta.

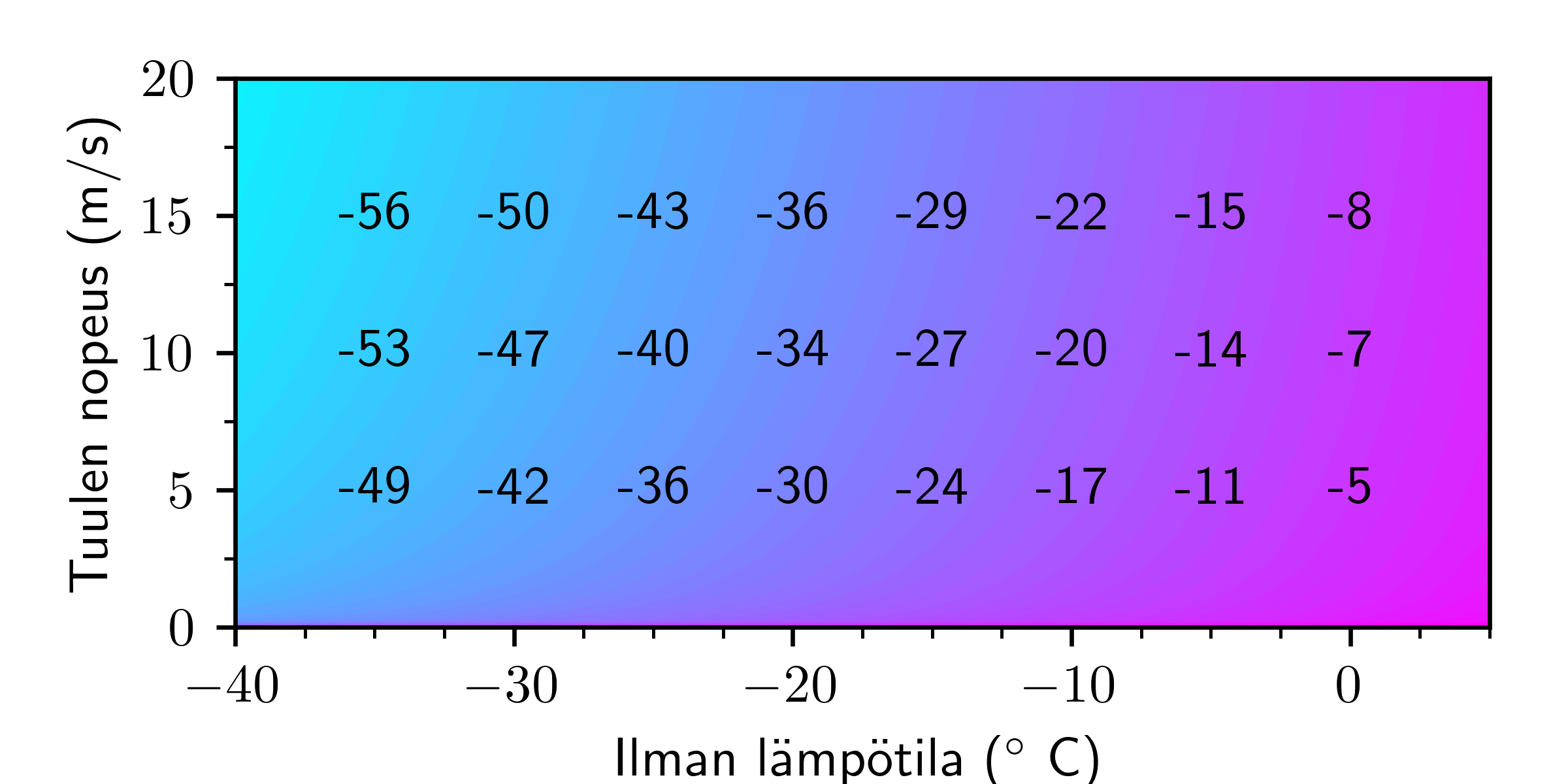
Kuva 2. Tuulen nopeudesta aiheutuva tuulen hyytävyys eri lämpötiloissa.

Joo, tätä juuri tarkoitin, mutta pointtini on juurikin että mistä nuo numerot tulevat. Mistä esimerkiksi tuo Wikipedian kaava tulee?

Ylläoleva kaava on kehitetty kokeiden, yritysten ja arvausten avulla. Ajan saatossa kaavoja on esitetty paljon muitakin. Tämä kaava on hieman ongelmallinen ja selvästikään fyysikot eivät ole sitä olleet kehittämässä. Ensiksi, kun törmäät kaavaan, jonka saatesanoina annetaan “suure x tulee esittää yksikössä y”, niin kaavaan voi suhtautua epäilevästi. Fysiikan avulla rakennetuissa lausekkeissa yksiköt ovat aina erottamaton osa yhtälöä. Tarkastellaan yksiköiden roolia toisen osion (Miksi polttoaineen kulutuksen yksikkö on neliömetri?) yhteydessä tarkemmin. Toiseksi, kaava ei toteuta yksinkertaisintakaan järjellisyystarkastelua (sanity check): jos tuulen nopeus on nolla, niin hyytävyyden tulisi tietenkin olla sama kuin ilman lämpötila; kaavan mukaan hyytävyys on kuitenkin mystinen

Ehkäpä kaavan kehittäjät ovat keskittyneet nimenomaan tuulisiin olosuhteisiin ja jättäneet hyytävyyden pienillä tuulenvireillä huomiotta. Kolmanneksi, edelliseen liittyen, oletus hyytävyyden ja ilman lämpötilan yhtä suuruudesta ($T_h=T_{ilma}$) edellyttäisi oudon ehdon tuulen nopeudelle.

No onpa outoa. Mutta kuitenkin se kuvaa koettua todellisuutta, jota fysiikkakin kuvaa. Miten siinä näkyvät fysiikan lait?

No siinäpä se, siitä on vaikea löytää fysiikkaa. Esimerkiksi tuo nopeuden $0{,}16$-potenssi on epätavallinen, mikä ilmentää kaavan empiirisyyttä; hyytävyyden on ehkäpä vain oletettu riippuvan lämpötilasta ja nopeuden jostakin potenssista, joka on sovitettu kokeelliseen dataan. 

Tällainen empiirisyys ei toki ole kiellettyä, mutta ei kovin havainnollistakaan, saati opettavaista. Fysiikan löytämiseksi meidän pitäisi laatia hyytävyydelle oma malli.

Onnistuisiko mallin laatiminen ihan tässä lennosta?

Niin… no miksipä ei! Tällä kurssilla esitetään paljon valmiita malleja, mutta ehkä tässä yhteydessä voisimme tosiaan käydä läpi miten sellaisen voisi tehdä itse. 

Tehdään niin! Pääsenpä seuraamaan fyysikkoa työssään.

Selvä. Tulossa voi olla hieman tavallista enemmän matematiikkaa, mutta pyritään pitämään maalaisjärki ja arkihavannot mukana mahdollisimman paljon.

Aloitetaan kysymyksellä: aistitko sinä suoraan ympäröivän ilman lämpötilaa?

Joo-o… Ei kun tämä on heti kompakysymys! En varmaankaan, koska koko kysymys ylipäätään liittyy hyytävyyteen.

Niin, me aistimme ensisijaisesti iholta poistuvan lämmönsiirtotehon. Jos esimerkiksi pidät oikeaa kättä kuumassa vedessä ja vasenta kättä kylmässä vedessä ja sitten tartut haaleaan metallitankoon, aistit eri käsilläsi eri lämpötilan. Oikea käsi aistii tangon kylmänä (koska iho on vedestä kuuma ja lämpöä siirtyy ihosta tankoon) ja vasen käsi aistii tangon kuumana (koska iho on vedestä kylmä ja lämpöä siirtyy tangosta ihoon).

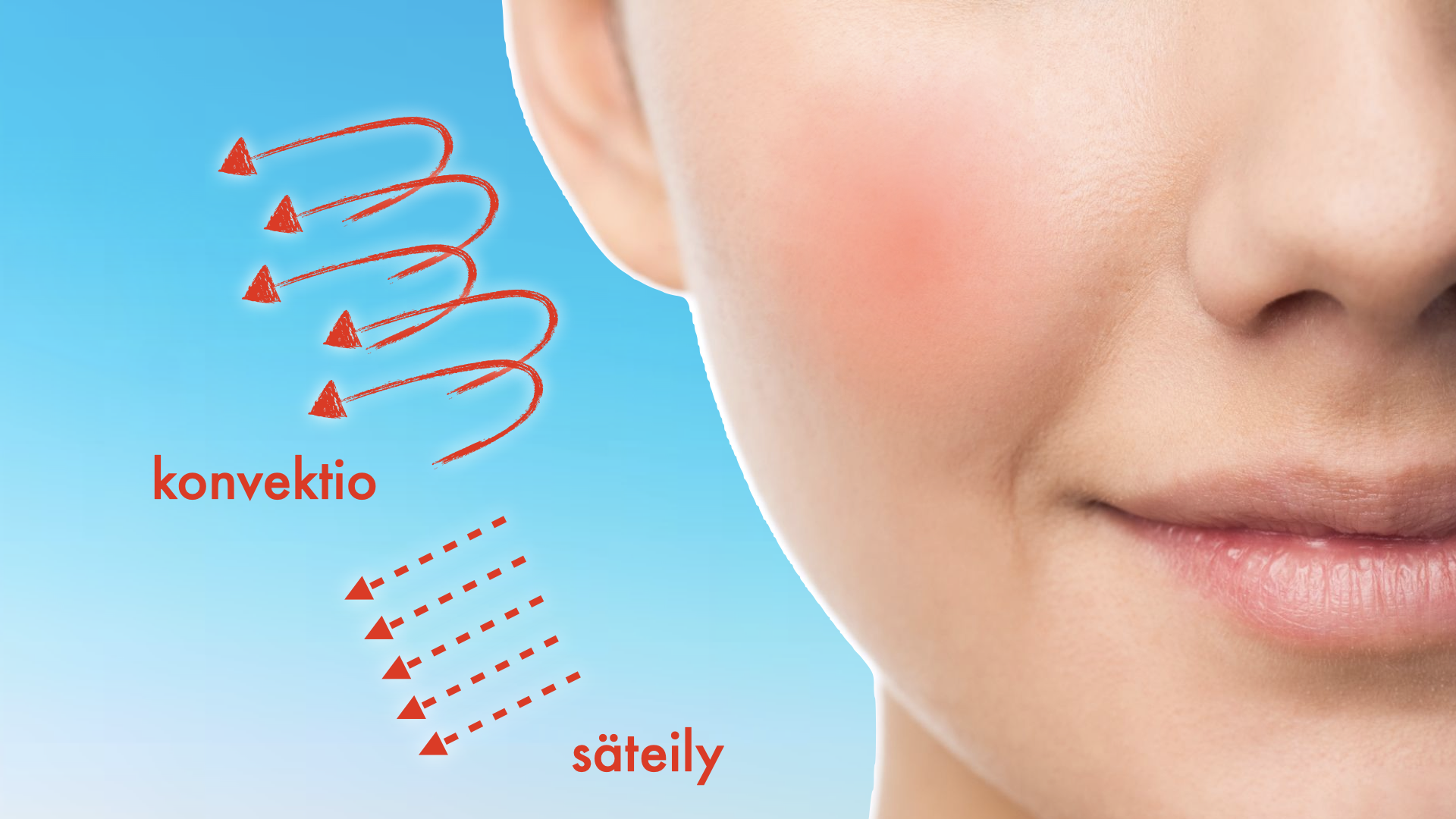
Kuva 3. Lämpötilan aistimuksen määrää pääosin iholta siirtyvä lämpöteho.

Tästä saamme fysikaalisen periaatteen hyytävyysmallin laatimiseen: lämmönsiirtoteho lämmönsiirtoteho lämpötilassa $T_h$ tuulen nopeudella nolla on sama kuin lämpötilassa $T_{ilma}$ tuulen nopeudella $v$. Kaksi eri tilannetta, joissa on eri lämpötilat ja eri tuulen nopeudet, mutta sama aistimus, koska lämmönsiirtotehot ovat yhtä suuret (Kuva 4). 

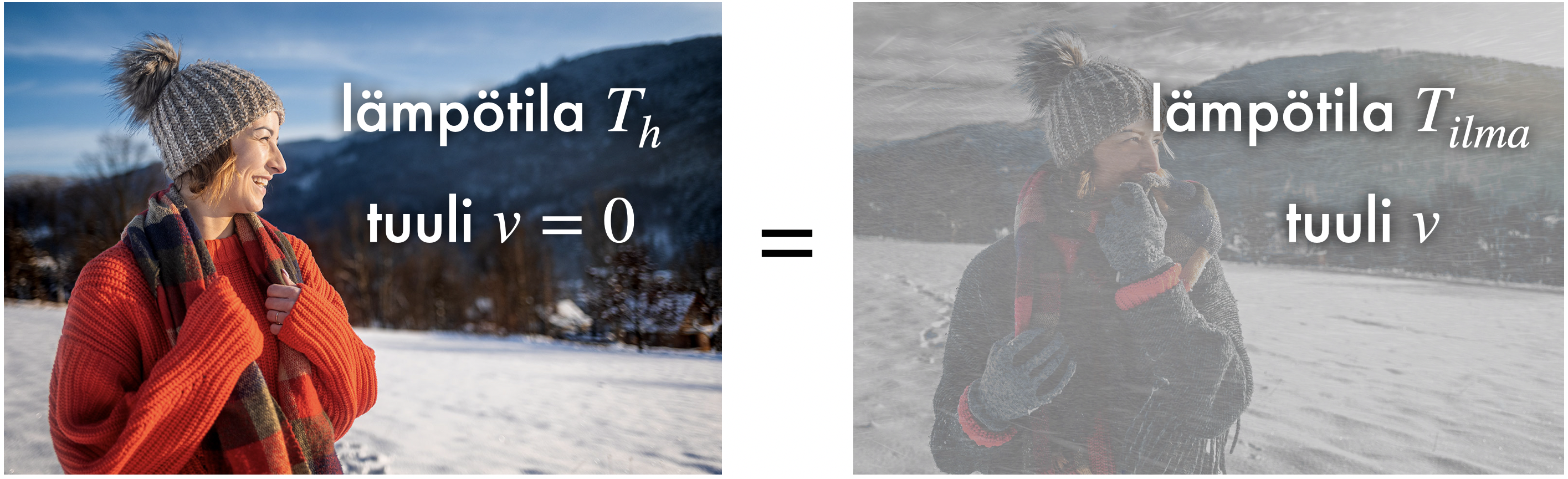
Kuva 4. Periaate hyytävyyden laskemiselle.

Tarkennetaan vielä sen verran, että tarkastellaan lämmönsiirtotehoa pinta-alaa kohden. Vaatetuksella ei siis ole merkitystä, sillä molemmissa tapauksissa (tuulella ja tyvenellä) oletetaan samanlainen vaatetus.

Nyt mallin rakentamisen suurin työ onkin jo tehty. 

Ei kai sentään.

Teknisesti ei, mutta periaatteellisesti kyllä. Olemme kehittäneet fysikaalisen periaatteen mallin taustalle; loppu on “ainoastaan” periaatteen huolellista toteuttamista käytännössä.

Kahvin jäähtymistä (osio: "Kannattaako maito lisätä kahviin heti vai myöhemmin?") pohtiessamme keskustelimme kolmesta lämmönsiirtotavasta, johtumisesta, konvektiosta ja säteilystä. Hyytävyyttä tarkasteltaessa meidän riittää tarkastella säteilyä ja konvektiota, johtumisen voimme unohtaa koska lämpö ei johdu iholta. Emme siis tarkastele lämmön johtumista vaatteiden läpi vaan lämmönsiirtoa suoraan iholta ilmaan. 

Kahvin jäähtymiskeskustelun pohjalta voimme todeta, että lämpötilassa $T_{ilma}$ ja tuulella $v$ iholta siirtyvä lämpö pinta-alaa kohden on 

Tässä $q_{sateily}$ on iholta säteilemällä poistuva lämpö. Se riippuu ihon lämpötilasta ja ympäristön lämpötilasta — mikä voi olla eri kuin ilman lämpötila (ympäristön lämpösäteily iholle voi olla lumihangen tai sinitaivaan lähettämää). Koska absoluuttisella lämpötilaskaalalla tuulen aiheuttama hyytävyys on pieni, voimme olettaa säteilemällä poistuvan lämpötehon olevan kaikissa tapauksissa yhtä suuri. Tämä oletus tehdään osin käytännön syistä, koska säteilytehon käsittely olisi hieman hankalaa.

Ahaa. Eli kuten keskustelimme johdannossa: rakennetaan malli, joka ei välttämättä ole täydellinen, mutta ratkaistavissa.

Siihen suuntaan joo. Kaavassamme esiintyvä termi $k(v)$ on konvektioon liittyvä lämmönsiirtokerroin, joka riippuu tuulen nopeudesta $v$. Suurempi tuulen nopeus → voimakkaampi lämmönsiirto → suurempi $k$. Siten voimme olettaa lämmönsiirtokertoimen olevan muotoa

missä $a$ ja $b$ ovat tuntemattomia vakioita (ja positiivisia myös, jotta lämmönsiirtoteho on oikeaan suuntaan tyvenessä ja kasvaa tuulen voimistuessa).

Hetkonen, mistä tuo lauseke $k$:lle oikein putkahti?

Fysiikassa mitä tahansa suuretta $y$, joka riippuu muuttujasta $x$, voidaan arvioida eli approksimoida eri tavoin. Alimmassa approksimaatiossa suure $y$ riippuu muuttujasta $x$ niin vähän, että voimme olettaa suureen olevan vakio $y=a$. Näinhän teimme jo yllä lämpösäteilyn tapauksessa; oletimme, että lämpösäteilyteho on vakio tuulesta riippumatta. Lineaarisessa approksimaatiossa riippuvuus ulkoisesta muuttujasta on lineaarinen, $y=a+bx$. Neliöllisessä approksimaatiossa riippuvuus muuttujasta on neliöllinen, $y=a+bx+cx^2$, ja niin edelleen. Lineaarinen approksimaatio on $k$:lle yksinkertaisin järkevä arvio, jonka voimme tehdä. Tilanteessa ulkoinen muuttuja $x$ on tuulen nopeus v, joten siitä tuo lauseke putkahti.

Voisimme mallintaa $k$:ta myös neliöllisesti, mutta tällöin mallista tulisi myös monimutkaisempi. Turha tehdä mallista alkujaan monimutkaista, mikäli se ei ehkä ole tarpeen. Vakioksi konvektiota emme voi olettaa, koska tällöin hyytävyyttä ei edes syntyisi.

Lopuksi edellä olleessa lämmönsiirron lausekkeessa $T_{iho}$ on ihon lämpötila.

Eli $37^\circ C$?

Sinnepäin, mutta ei aivan. Viima viilentää ihon pintakerrosta, jolloin ilman ja ihon välinen lämpötilaero ja sen myötä myötä myös lämmönsiirtoteho pienenevät. Meidän tulee siis olettaa myös ihon lämpötila riippuvan  ilman lämpötilasta ja samanaikaisesti myös tuulen nopeudesta. Yksinkertaisin tapa kuvata ihon lämpötilaa on siten 

missä kertoimet $A$:sta $D$:hen ovat tuntemattomia vakioita. 

Ja tämä lauseke tupsahti nyt samalla logiikalla kuin lämmönsiirtokertoimen lauseke?

Juuri niin. Eikä tässä ole mitään mystiikkaa; muunnamme ainoastaan maalaisjärkisen pohdiskelun matemaattiseksi lausekkeeksi. Lauseketta voidaan lisäksi yksinkertaistaa lisäpohdinnoilla. Voimme nimittäin vaatia, että ihon lämpötila ei saa riippua tuulesta, mikäli ilman lämpötila on ihon normaalilämpötila $T_n\approx 37^\circ C$.

Aivan, $37^\circ C$ -lämpöisessä ilmassa lämpöä ei siirry iholta vaikka kuinka tuulisi, joten ihon lämpötila pysyy vakiona.

Jep! Tästä voikin päätellä ihmisten olevan ongelmissa ulkolämpötilan noustessa näin korkeaksi. Vaatimuksemme ansiosta ihon lämpötilan lauseke yksinkertaistuu muotoon

$T_{iho}(v,T_{ilma})=T_n-(C+Dv)(T_n-T_{ilma})$.

Kannustan sinua tekemään tämän pienen yksinkertaistamisen itse kynällä ja paperilla. Lausekkeen muodosta näemme, että $T_{iho}=T_n$ tuulesta riippumatta, kun $T_{ilma}=T_n$.

Nyt meillä onkin palaset kasassa ja voimme soveltaa aiemmin päätettyä kuvan 3 perusperiaatetta:

tai toisin sanoen 

eli

Voimme huomata, että lämpösäteily on yhtälön molemmin puolin sama, joten se kumoutuu pois. Tehtäväksemme jää ratkaista tästä lausekkeesta $T_h$ tuulen nopeuden ja ilman lämpötilan avulla lausuttuna (suosittelen tekemään sen myös itse!). Tulokseksi saamme

missä $\alpha=b/a$ ja $\beta=D/(1-C)$ ovat aiemmin esiteltyjen tuntemattomien vakioiden avulla lausuttuja uusia tuntemattomia vakioita. 

Malleja kehitettäessä kannattaa usein pysähtyä tarkastelemaan, että lausekkeet ovat järkeviä. Tarkastellaanpa siis lauseketta ja sen ominaisuuksia kriittisesti (Video 1).

Video 1. Hyytävyyden lausekkeen kriittistä tarkastelua eri näkökulmista.

Summa summarum, lausekkeemme tuulen hyytävyydelle vaikuttaa monin tavoin järkevältä ja toteuttaa maalaisjärkiset reunaehdot. Kuitenkaan lauseketta ei olisi voinut keksiä ja perustella suoraan lonkalta

Joo, nuo vaikuttaa kyllä järkeviltä, vaikka ei tuollaista tosiaan voi keksiä omasta päästä. Ja ennen kaikkea, nyt meillä on lauseke joka on ymmärrettävissä ja rakennettu tunnetuista lähtökohdista. Mutta ei meillä kyllä ole vielä mitään konkretiaa; mitä nuo tuntemattomat vakiot ovat? Ja mistä tiedämme, että malli ylipäätään toimii? Ei kai järkevältä tuntuminen todista mallin toimivuutta?

Ei. Fysiikassa mallin toimivuuden määrää se kuinka hyvin se kuvaa havaintoja. Eli mallin rakentamisessa meiltä puuttuu vielä keskeinen osio, mallin (tuntemattomien vakioiden) sovittaminen ja vertaaminen havaintoihin.

Meillä ei ole nyt mahdollisuutta tehdä laajoja kokeita, mutta ehkä voisimme tehdä ”virtuaalisia kokeita” käyttämällä alkuperäistä empiiristä lauseketta. Valitaan siis eri ilman lämpötiloja ja tuulen nopeuksia ja ”mitataan” hyytävyys käyttämällä empiiristä kaavaa. Otetaan vaikkapa lämpötilat viidestä asteesta miinus neljäänkymmeneen pakkasasteeseen (asteen välein) ja tuulen nopeudet nollasta viiteentoista metriin sekunnissa ($m/s$ välein). Sitten sovitetaan vakiot $\alpha$ ja $\beta$ siten, että mallimme toistaisi nämä ”kokeelliset” hyytävyydet mahdollisimman tarkasti. Kun annamme sovittamisen tietokoneen huomaan, saamme vakioille arvot $\alpha=0.056\; s/m$ ja $\beta=0.020\; s/m$. Lopullinen mallimme hyytävyydelle on siis

Ja entä mallin toimivuus..?

Kuvassa 5 on vertailtu kehittämämme mallin ja empiirisen mallin hyytävyyksiä. Sanoisin, että mallimme kuvaa tuulen vaikutusta ilman hyytävyyteen kohtuullisen hyvin. 

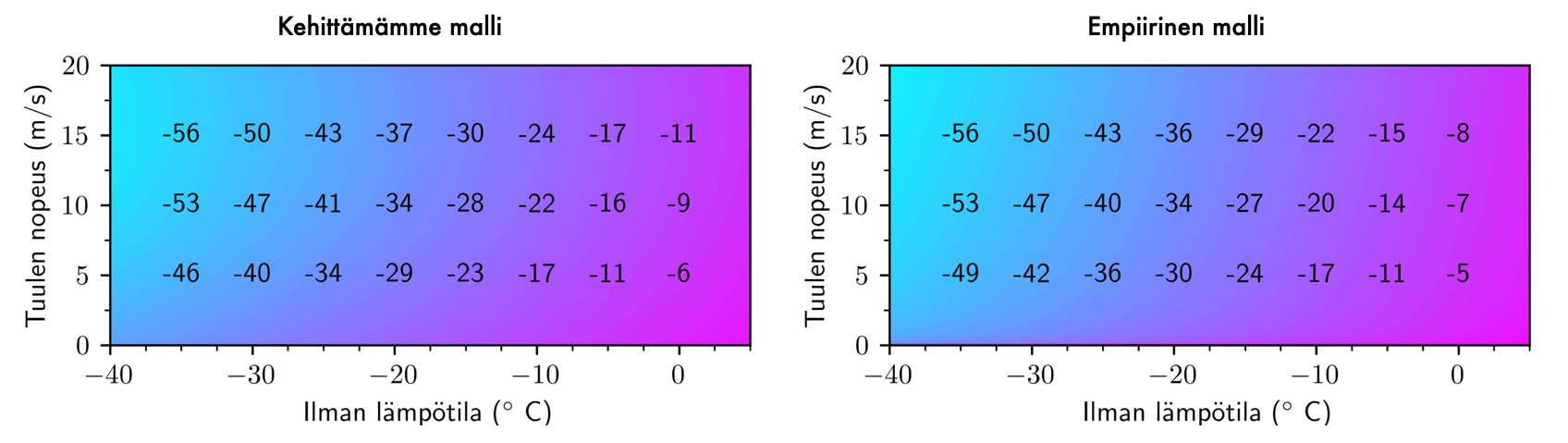
Kuva 5. Tuulen hyytävyys laskettuna kehittämällämme mallilla (vasen) verrattuna empiiriseen malliin (oikea, sama kuin kuva 2).

Mutta joitakin eroja löytyy kyllä.

Kyllä. Mutta suurelle osalle kuvan mittauspistaistä, etenkin pienillä tuulilla ja maltillisilla pakkasilla, hyytävyyksien erot ovat vain asteen-pari. Keskimääräinen absoluuttinen lämpötilaero "mitatuille" hyytävyyksille on vain $0{,}38$ astetta. Mallimme toimii parhaiten pienillä tuulen nopeuksilla kuten on odotettua, sillä lineaarisina approksimaatioina kehittämämme $k(v)$:n ja $T_{iho}$:n lausekkeet olivat lähtökohtaisesti rakennettu toimimaan vain riittävän pienillä nopeuksilla. Esimerkiksi hyytävyyden lausekkeesta voi nähdä, että riittävän suurilla tuulen nopeuksilla hyytävyys alkaa pienenemään, mikä ei ole järkevää; tämä johtuu siitä että suurilla tuulen nopeuksilla iho jäähtyy liian paljon, minkä vuoksi lämmönsiirtoteho pienenee. Tämä on odotettua, sillä käytännössä kaikilla malleilla on rajattu voimassaoloalue.

Liittyykö voimassaoloalue videon lopussa esitettyyn ehtoon parametreille?

Liittyy. Videolla mainittu ehto nopeudelle oli $v$, josta saatujen parametrien avulla tulee $v < 16\; m/s$. Tämä vaikuttaa jokseenkin järkevältä tulokselta. Tätä kovemmilla tuulilla mallin toimivuus on siis kyseenalainen.

Tosin meillä on vielä eräs tärkeä näkökulma tarkastettavana. Meidän tulee nimittäin varmistaa, että malli toimii oikeista syistä. Suurella määrällä erilaisia sovitettavia parametreja voi saada minkä tahansa mallin kuvaamaan havaintoja,

Ai niin kuin että malli antaa oikeita numeroita, mutta fysiikka on vinksin vonksin?

Hyvin sanottu. Tätä varmistelua varten meidän tulee ottaa pari askelta taaksepäin. Kokeisiin sovittamisen kannalta vakiot $\alpha$ js $\beta$ ovat siis vain parametreja. Me kuitenkin haluamme, että vakio $\alpha=b/a$ oikeasti kuvaa lämmönsiirtokerrointa $k(v)=a+bv$ järkevästi ja että vakio $\beta=D/(1-C)$ kuvaa ihon lämpötilaa $T_{iho}(v,T_{ilma})=T_n-(C+Dv)(T_n-T_{ilma})$ järkevästi.

Katsotaan ensin lämmönsiirtokerrointa. Sovituksesta saamme, että se on verrannollinen tekijään $(1+v\cdot 0.056 \; \text{s/m})$. Käyttämällä riippumattomasta lähteestä saatua arviota lämmönsiirtokertoimen nopeusriippuvuudelle, voimme huomata että sovittamamme vakio $\alpha$ kuvaa nopeusriippuvuutta lineaarisen mallin puitteissa järkevästi (kuva 6).

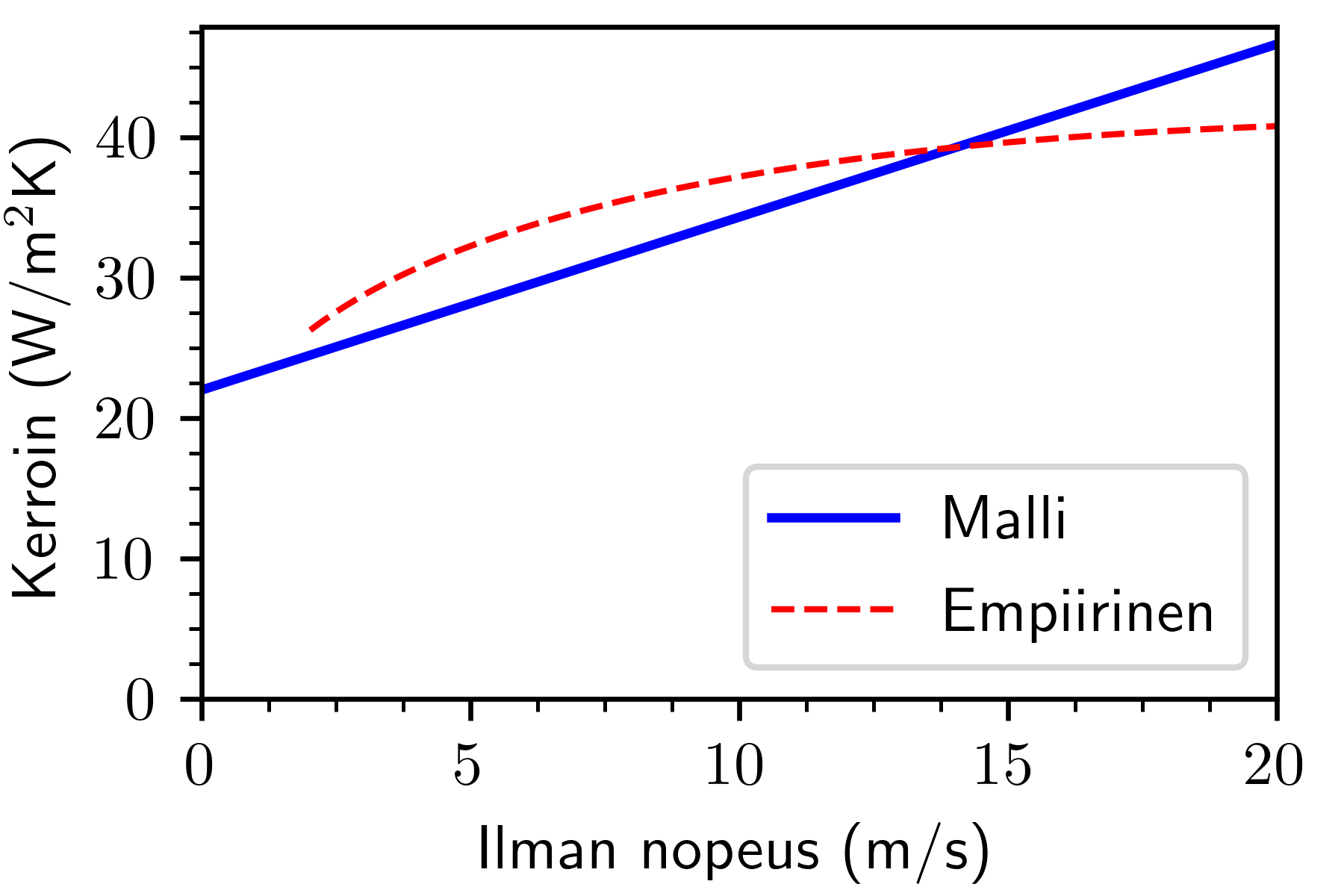
Kuva 6. Lämmönsiirtokerroin nopeuden funktiona (punainen, EngineeringToolbox), verrattuna mallimme antamaan nopeusriippuvuuteen (sininen).

Sovittamalla tuntemattoman etukertoimen, saamme ihon lämmönsiirtokertoimeksi on $k(v)=22\cdot (1+v\cdot 0.056\; \text{s/m})$ W/m$^2$K. Kertoimen lineaarisuus sinänsä oli oma valintamme, mutta muutoksen suuruuden se antaa silti kohtalaisen hyvin.

Miksi muuten emme käyttäneet tuota lämmönsiirtokerrointa jo alussa?

Lämmönsiirtokerroin liittyy ilman ja pinnan välisen rajapinnan ominaisuuksiin. Iholle lämmönsiirtokerrointa on vaikea mitata suoraan ja myös mitatun kertoimen tapauksessa meidän olisi pitänyt laatia nopeusriippuvuudelle jokin yksinkertainen lauseke. Tällöinkin lineaarinen riippuvuus olisi ollut yksinkertaisin valinta. Riippumattoman lähteemme tilanne ei suoraan liity lämmönsiirtoon iholta, mutta voimme silti olla tyytyväisiä, että kertoimen käyttäytyminen yleisellä tasolla tukee mallimme toimivuutta.

Ja vielä toinen varmistus, eli kuvaavatko sovitetut parametrit ihon lämpötilaa järkevästi? Sovittamamme parametrit eivät anna täsmällistä arvoa ihon lämpötilalle, mutta käytettävissämme on vielä yksi vapaa parametri sovittamista varten. Voimme sovittaa parametrin hyödyntämällä tietoja siitä miten paleltumariski kasvaa lämpötilojen ja tuulien mukana. Mallimme kannalta voimme määritellä paleltumariskin kasvamisen tarkoittavan ihon lämpötilan painumista pakkasen puolelle. Sovittaminen antaa ihon lämpötilalle lausekkeen

Kun ratkaisemme lausekkeesta tuulen nopeuden, jolla annetussa lämpötilassa ihon lämpötila menee nollaan, saamme paleltumisvaaralle kuvaan 7 merkityn trendin. Tämä arvio on kohtuullisen lähellä hyytävyyskarttoihin piirrettyjen paleltumavaaran rajojen kanssa.

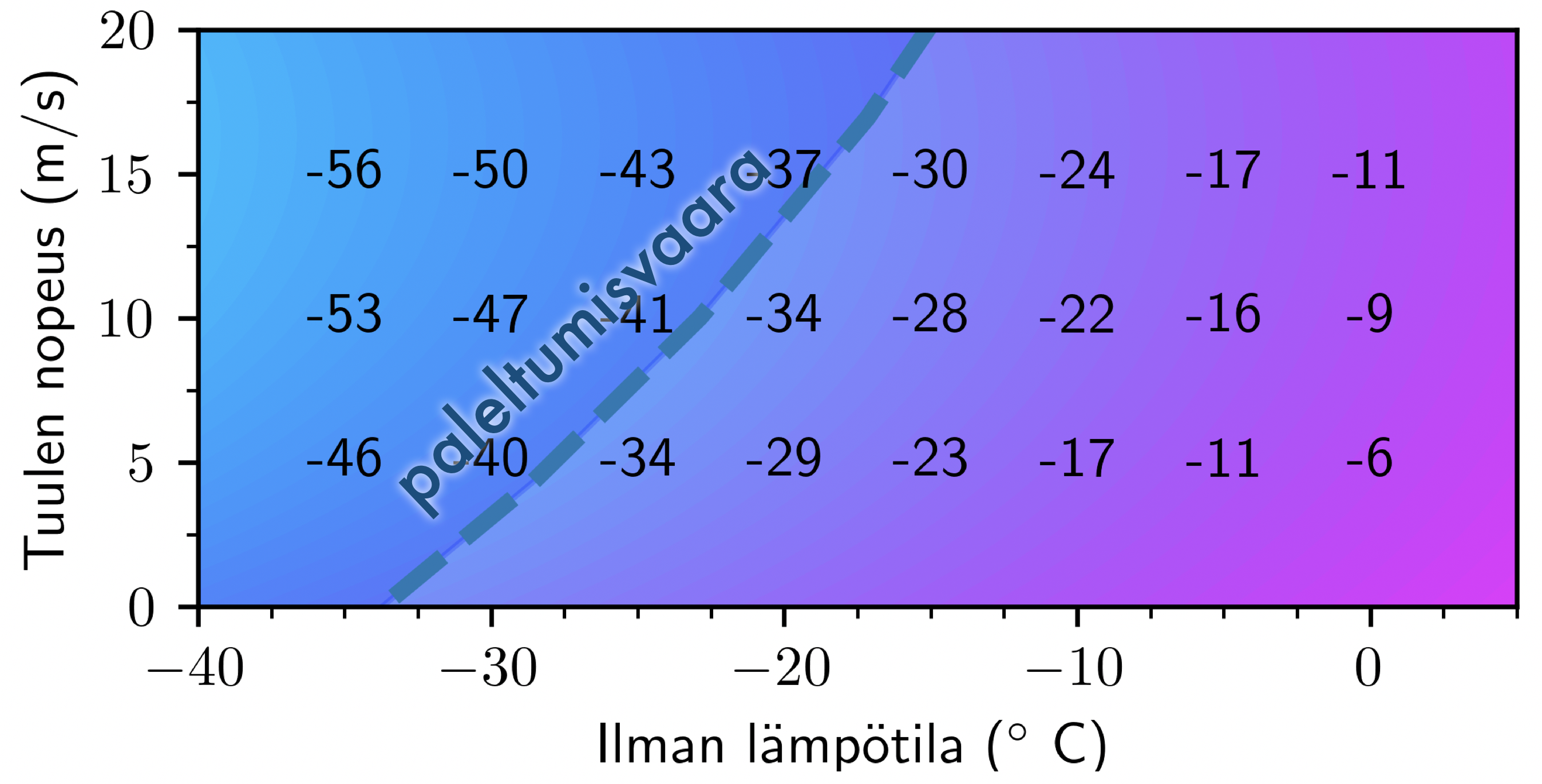
Kuva 7. Katkoviiva esittää rajaa, jolla ihon lämpötila menee pakkasen puolelle ja riski paleltumien syntymiselle on suuri.

Kaikkiaan siis mallin sovituksen liittyen sekä lämmönsiirtokerroin että ihon lämpötila käyttäytyvät järkevästi. Voimme siis todeta, että malli vaikuttaisi toimivan oikeista syistä ja olevan siten kelpo fysikaalinen malli tuulen hyytävyydelle. Ja koska malli toimii oikeista syistä, niin sitä voisi lähteä parantamaan esimerkiksi kuvaamalla lämmönsiirtokerrointa nopeuden suhteen neliöllisesti. Neliöllisyys vain toisi yhden sovitusparametrin lisää.

Entä kosteus, eikö sekin vaikuta? Kostealla ja tuulisella säällä pakkanen menee oikein luihin ja ytimiin. Ja sekin kuinka kauan annamme tuulen vaikuttaa.

Erinomaisia huomiota. Meidän mallimme ja empiirinen kaava jättävät molemmat kosteuden vaikutuksen täysin huomiotta. Kosteuden haihtuminen iholta aiheuttaa erittäin merkittävän lämmönsiirtotehon. Kosteuden vaikutus liittyy sekä suhteelliseen että absoluuttiseen kosteuteen, ja sen tarkastelu vaikeuttaisi tilannetta huomattavasti. Lisäksi kosteuden lisäämällä hyytävyydestä ei voisi tehdä yksinkertaista taulukkoa. Myös säteilyn vaikutus voi olla huomattava, minkä voimme kokea kasvoillamme kevättalven ensimmäisinä aurinkoisina päivinä. Kuvan 6 mukaan konvektion lämmönsiirtoteho on parikymmentä wattia neliömetriä ja astetta kohden. Jos mittari on nollassa, ilman ja ihon lämpötilaero on nelisenkymmentä astetta ja konvektion lämmönsiirtoteho $0{,}8$ kW neliömetriä kohden. Auringon säteilyteho parhaimmillaan on $1{,}4$ kW neliömetriä kohden — joten tokihan aurinko tuntuu lämpimältä!

Kaiken lisäksi hyytävyyden tunteeseen liittyy myös mainitsemasi aikaskaala. Ihon lämpötila ei ole vakio, vaan riippuu ulkona olon ajasta. Siten myös hyytävyyden tunne ja etenkin paleltumisriski riippuu siitä kauanko ulkona ollaan.

Hyytävyyden monimutkaisuuden vuoksi esimerkiksi ilmatieteen laitos on lakannut julkaisemasta pelkästään tuuleen liittyviä hyytävyystaulukoita. Sen sijaan sääennustukset sisältävät suoraan ”tuntuu kuin” -lämpötilan hahmoineen (kuva 8). Pelkän tuulen määräämänä hyytävyysarvioon voi suhtautua suuntaa-antavana. Joka tapauksessa on erittäin hyödyllistä ymmärtää hyytävyyden taustalla olevaa fysiikkaa. Jonakin päivänä tietämys saattaa pelastaa korvannipukat paleltumiselta.

Kuva 8. Lämpötila hahmon ohessa kertoo ”tuntuu kuin” -lämpötilan.