Aamulla kun istahdin juomaan kahvia, kaverini soitteli ja juttelimme hetken. Puhelun jälkeen kahvi oli jo kovin haaleaa ja aloin pohtimaan kahvin jäähtymistä. Olisiko kahvi ollut lämpimämpää, jos olisin sittenkin lisännyt maidon vasta puhelun jälkeen?

Selvä, eli satuin tekemään oikein. Mutta miksi näin?

Varmistetaan ensin, että meillä on jäähtymisen käsittelyyn yhteinen kieli. Palautetaan vielä mieliin erilaiset lämmönsiirtotavat:

Arkisia esimerkkejä lämmönsiirtomekanismeista ovat kuuma lusikka teekupissa (johtuminen), kuuma ilma kynttilän yläpuolella (konvektio) ja auringon ottaminen (lämpösäteily) (Kuva 1).

Kuva 1: Lämmönsiirtoa johtumalla, konvektiolla ja säteilemällä.

Tarkastellaan nyt eri lämmönsiirtotapojen merkitystä kahvin jäähtymisessä.

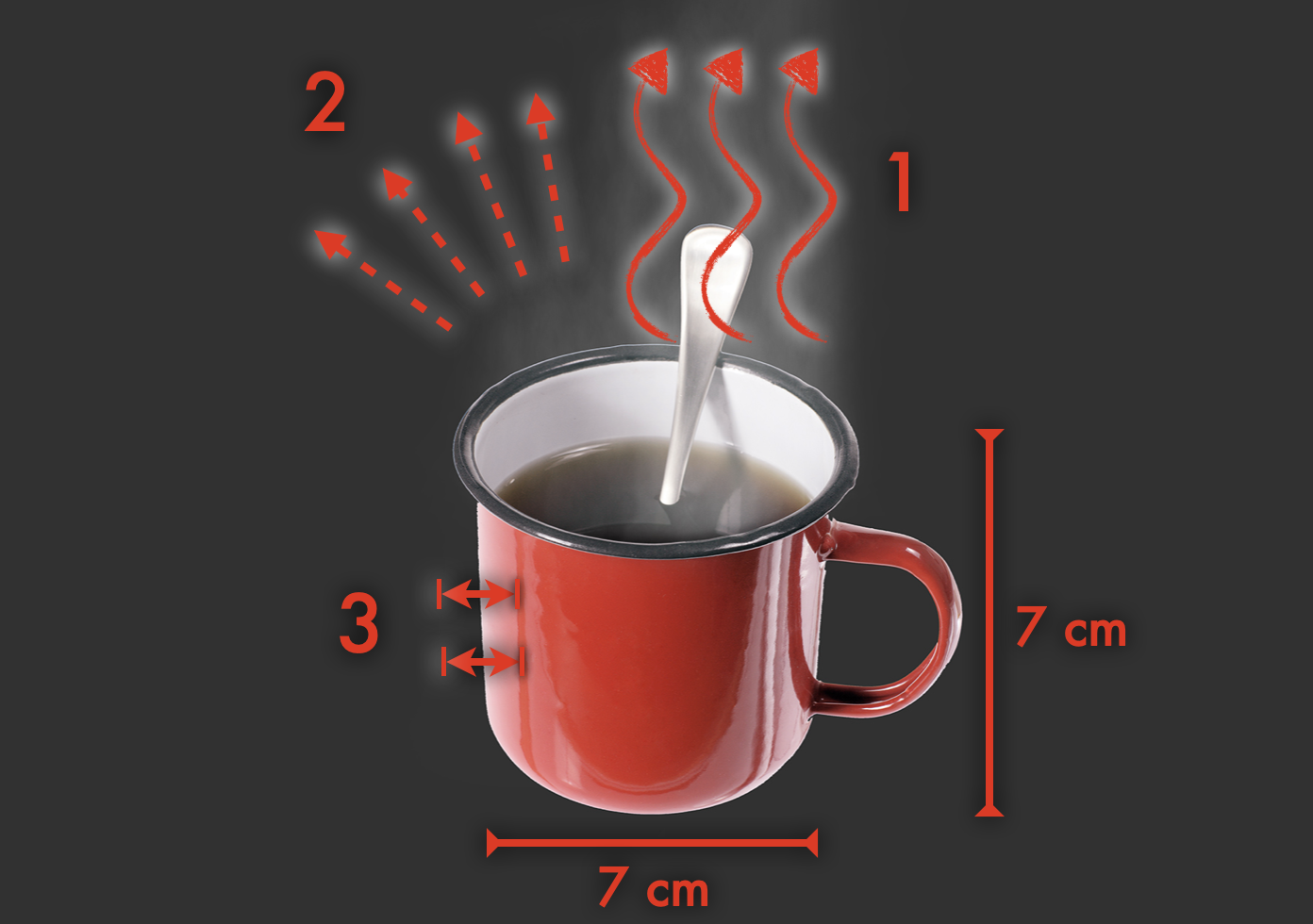
Kuva 2. Lämmönsiirtomekanismit kahvin jäähtymisestä: 1) lämpö siirtyy konvektiolla ilmaan, 2) lämpö säteilee kahvista ympäristöön, 3) lämpö johtuu kahvista kuppiin ja lusikkaan (systeeminä on siis pelkkä kahvi; kuppi ei kuulu systeemiin).

Aloitetaan tarkastelu johtumisesta. Kahvia kaadettaessa kahvi on kuumaa ja kuppi on kylmä. Siispä lämpö siirtyy kuumasta kahvista kylmään kuppiin johtumalla. Lämmön siirtyessä kuppi lämpenee, sitä nopeammin mitä pienempi on kupin lämpökapasiteetti — eli karkeasti mitä ohuempi on kupin seinämä. Lämmönsiirtoteho johtumalla on verrannollinen kahvin ja kupin välisen rajapinnan pinta-alaan $A_{kuppi}\approx 150\; cm^2$ ja ainakin heti kaatamisen jälkeen verrannollinen myös kahvin ja kupin lämpötilaeroon $T_{kahvi}-T_{kuppi}$. Siten lämmönsiirtoteho johtumalla on

missä $k_j$ on lämmönsiirtokerroin, joka on ominainen kahvin ja kupin rajapinnalle. Kuumaa ($\sim 70^\circ$C) kahvia huoneenlämpötilaiseen posliinikuppiin kaadettaessa hetkellinen lämmönsiirtoteho voi olla hetkellisesti melko suuri. Tämän  vuoksi hyvissä kahviloissa baristat minimoivat tämän lämmönsiirron lämmittämällä kupin valmiiksi. 

Eli baristankin työ sisältää fysiikkaa?

Ehdottomasti! Ja varmasti myös kemiaa sekä ehdottomasti psykologiaa. Toisaalta johtumisteho kuppiin pienenee hyvin nopeasti kupin lämmetessä.

Mutta eikö lämpö johdu ilmaan myös kahvin pinnalla? 

Jossakin mielessä kyllä, mutta tällöin prosessi kuitenkin luokitellaan konvektioksi. Kahvin pinnalla lämpöä siirtyy vesimolekyyleistä ilman molekyyleihin, mutta lämmennyt ilma ei pysy paikoillaan kuten kupin seinämä, vaan kohoaa huoneilmaa keveämpänä ylöspäin. Siten lämpö siirtyy konvektiolla huoneilmaan. Siirtoteho on suoraan verrannollinen kahvin pinnan pinta-alaan $A_{kahvi}\approx 40\; cm^2$. Pinta-alan suoraan verrannollisuus on uskottavaa, sillä esimerkiksi kahdesta kahvikupista lämmönsiirto konvektiolla on luonnollisesti kaksinkertainen. Konvektio on melkoisen monimutkainen ilmiö, mutta sitä voi mallintaa yksinkertaisella Newtonin lämmönsiirtolailla. (Tällä lailla ei ole tekemistä Newtonin liikelakien kanssa!) Lain mukaan siirtoteho on verrannollinen kahvin ja huoneilman lämpötilojen erotukseen, aivan kuten lämmön johtumisessa. Siten lämmönsiirtoteho konvektiolla on

missä $k$ on lämmönsiirtokerroin, jonka suuruus riippuu ilman liikkeestä; vapaassa konvektiossa kerroin on pienempi (esim. $\sim 5\;W/m^2K$) ja pakotetussa konvektiossa (eli kahvia puhaltaessa) kerroin on suurempi (esim. $\sim 50\;W/m^2K$). Vapaalla konvektiolla lämmönsiirtoteho kuumalle kahville on noin $\sim 1\; W$, puhaltamalla $\sim 10\; W$.

Newtonin lämmönsiirtolain voi ymmärtää kahvin ja ilman rajapinnan mikroskooppisella tarkastelulla. Kahvin molekyyleillä eli käytännössä vesimolekyyleillä on keskimäärin enemmän energiaa kuin ilman molekyyleillä (enimmäkseen $N_2$-molekyylejä). Siten keskimäärin nopeammat vesimolekyylit antavat rajapinnan törmäyksissä energiaa hitaille ilman molekyyleille. Energiaa siirtyy törmäyksissä sitä enemmän, mitä suurempi on molekyylien keskimääräisen energian erotus; erotus puolestaan on suoraan verrannollinen lämpötilojen erotukseen (koska molekyylien keskimääräinen energia on verrannollinen absoluuttiseen lämpötilaan). Samoin voi perustella lämmönsiirtoa johtumisessa.

Konvektio on muuten tärkeää myös kupin sisällä: kahvin lämpötila säilyy tasaisena, kun nesteessä kiertää lämpötilaerojen spontaanisti synnyttämiä sisäisiä konvektiovirtoja. Kahvin sekoittaminen lusikalla on myöskin yksinkertaisesti kahvin sisäistä pakotettua konvektiota!

Ja konvektiota tapahtuu myös kupin pinnasta.

Kahvikupin osalta kyllä, mutta kahvin osalta ei. Tarkasteltava systeemi on kahvi, joten tarkastelemme lämmönsiirtoa vain kahvin osalta. Kupin pitäminen viileänä vaikkapa kylmillä käsillä tietenkin nopeuttaa lämmönsiirtoa kahvista kuppiin edelleen, mutta tästä näkökulmasta tarkasteltavana olisi eri systeemin tarkastelu (eli systeemi=kahvi+kuppi).

Joo, niinpä kai. Entä muuten jos kahvin pinnalla on vaahtoa?

Tuo on hyvä nosto. Lämmönsiirto konvektiolla vaahdon pinnalta tapahtuu yllä olevalla periaattella, erona vain se, että vaahdon ja ilman rajapinnassa ja vaahdon ja kahvin rajapinnassa voi olla suuri lämpötilaero, koska ilmakuplien vuoksi vaahto itsessään johtaa  lämpöä erittäin huonosti. Ikään kuin kahvin pinnalla olisi eristävä styroksilevy. Vaahdon lämpöä eristävä kyky lienee syynä myös tapaan valmistaa cappuccino — se säilyy lämpimämpänä kauemmin ja pitkittää kahvinautintoa! 

Keskitytään tarkastelussamme kuitenkin kahviin ilman vaahtoa.

Kuva 3. Ilman vaahtoa kahvin pinnan lämpötila korkea ja lämmönsiirtoteho suuri (vasen). Vaahdon kanssa kahvin pintalämpötila (joka on vaahdon alla!) on korkea, mutta lämmönsiirto vaahtoon pieni (oikea). Lähes koko lämpötilaero kuumasta kahvista huoneilmaan on vaahdon ala- ja yläpinnan välillä.

Lämmönsiirto johtumalla ja konvektiolla tuntuvat tutuilta, mutta lämpösäteily arjessa ei niinkään. 

Tuo on ymmärrettävää. Me ihmiset aistimme lämmön siirron kokonaisuutena, mutta lämmönsiirtomekanismin eritteleminen arjessa voi olla vaikeaa.

Lämpöä kuitenkin siirtyy kahvista ympäristöön myös säteilemällä. Myös säteilyteho on suoraan verrannollinen kahvin pinta-alaan $A_{kahvi}$. Siihen yhtenevyys johtumiseen ja konvektioon loppuukin, sillä kahvin pinnan säteilemä energia on verrannollinen pinnan absoluuttisen lämpötilan neljänteen potenssiin. Tätä säteilyä kuvaa Stefan-Boltzmannin laki

missä $T$ on säteilevän pinnan lämpötila, $A$ sen pinta-ala ja $\sigma=5,6\times 10^{-8}$ $Wm^{-2}K^{-4}$ on luonnonvakio nimeltään Stefan-Boltzmannin vakio. (Oletamme tässä pinnan emittoivan säteilyä täydellisesti.) Tämä säteilyteho ei sisällä ainoastaan lämpö- eli infrapunasäteilyä, vaan kaiken säteilyenergian, mukaan lukien näkyvän valon, ultraviolettisäteilyn ja kaikki muutkin aallonpituudet.

Eli 40$^\circ C$ kappale säteilee 16 kertaa enemmän kuin 20$^\circ C$ kappale?! 

Ei, sillä neljännen potenssin verrannollisuus on nimenomaan absoluuttiseen lämpötilaan, lämpötilaan mitattuna Kelvin-asteikolla, jonka nollakohta on -273,15$^\circ$C. Siten 40$^\circ C$ pinta säteilee $(313~K/293~K)^4=1,3$ kertaa enemmän kuin 20$^\circ C$ pinta.

Mistä tuollainen laki tulee?

Säteilyn syntymisen voi hahmottaa karkeasti vaikkapa seuraavasti. Aineen sisällä atomien ytimet ja elektronit ovat lämpöliikkeen vuoksi jatkuvassa liikkeessä ja törmäilevät toisiinsa. Törmäily tarkoittaa kiihtyvää liikettä, mikä synnyttää sähkömagneettista säteilyä eli fotoneita. Samoin kun törmäilyissä syntyy fotoneita, törmäilyt myös absorboivat fotoneita. Materiaalin pinnan ulkopuolella ei kuitenkaan ole ainetta, joka aineessa syntyneitä fotoneita absorboisi; tällöin fotonit karkaavat pinnasta ulospäin, mikä havaitaan lämpösäteilynä. Mitä suurempi lämpötila, sitä enemmän aineen varatut rakenneosaset törmäilevät, sitä enemmän aineessa syntyy fotoneita, ja sitä voimakkaammin pinta säteilee fotoneita ulospäin. Siten voi ymmärtää säteilyn voimistumisen lämpötilan kasvaessa.

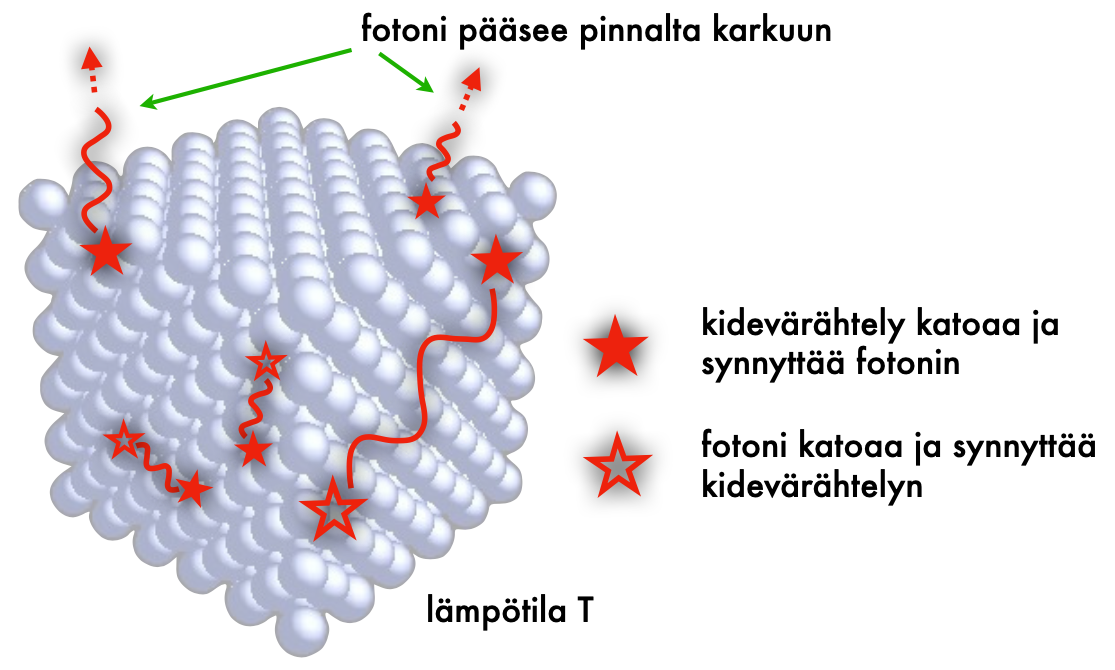
Kuva 4. Lämpötilassa $T$ olevan materiaalin sisällä tapahtuu jatkuva prosessi, jossa kidevärähtelyt katoavat (annihiloituvat) ja synnyttävät fotoneita ja fotonit puolestaan katoavat ja synnyttävät kidevärähtelyitä. Pinnan lähellä syntyneet fotonit saattavat ennen annihiloitumistaan ehtiä livahtamaan karkuun pinnan ulkopuolelle.

Entä tuo neljäs potenssi tulee? Sellaisia harvoin näkee fysiikan kaavoissa.

Tuo on muuten totta, fysiikan kaavoissa neljäs potenssi on harvinainen. Tämän kurssin puitteissa en kuitenkaan osaa perustella ilman kvanttimekaniikkaan nojautumista. Jätetään perustelut myöhempiin fysiikan opintoihin.

Mainitsit muuten, että lämmönsiirto säteilemällä tuntuu arjessa oudommalta, mutta eikö mieleen tule mitään tuttua?

Mitä ajat takaa? Ai, eikun höh — aurinko tietenkin!

Jep. Auringon säteilemä teho voidaan siten arvioida myös Stefan-Boltzmannin lailla. Auringon pintalämpötila on $5778\;K$ ja säteilyteho Stefan-Boltzmannin lain mukaan $63\; MW/m^2$; $r_s=700\; 000$ km säteisenä pallona Auringon kokonaisteho on $3{,}8\cdot 10^{26}\; W$. Aurinko säteilee tasaisesti kaikkiin suuntiin, joten maan etäisyydellä $R=150\cdot 10^6\; km$ auringon säteilyteho on $1{,}4\; kW/m^2$ (auringon koko teho jaettuna $R$-säteisen pallopinnan läpi). 

Hei — eikös tuo ole se aurinkovakio?

Sepä se, eli aika mielenkiintoinen ja yllättävä yhteys kahvikupista auringon säteilytehoon Maassa. Mutta tehdäänpä tähän liittyen vielä yksi mielenkiintoinen laskutoimitus, silläkin riskillä että keskustelumme hieman rönsyilee. Maapallon säde $r=6371\; km$, joten auringon maapallolle säteilemä kokonaisteho on $174$ petawattia (aurinkovakio kerrottuna maapallon poikkipinta-alalla $\pi r^2$ Auringosta katsottuna). Toisaalta maapallo itsessään on lämpöä säteilevä kappale kuten Aurinkokin. Maapallon keskimääräinen pintalämpötila on $\sim 5^\circ C$ ja säteilyteho Stefan-Boltzmannin mukaan $2{,}2\; mW/m^2$; $r$-säteisenä pallona Maapallolta poispäin lähtevän säteilyn kokonaisteho on $170$ petawattia — eli käytännössä sama kuin auringon säteilemä teho maapallolle! (Kosminen $2{,}7\; K$ taustasäteily maahan voidaan jättää tässä huomiotta.) Planeettojen pintalämpötila ja niin kutsutun elämän vyöhykkeen olemassaolo määräytyykin etäisyydestä aurinkoon juuri tähän tyyliin.

Kuva 5. Jotta maapallo ei kuumenisi jatkuvasti, sen avaruuteen säteilemä energian täytyy olla yhtä suuri auringosta maahan säteilemä kokonaisenergia. Tämä yhtäsuuruus määrää maapallon pintalämpötilan ja sitä myöten elämän vyöhykkeen eli elämälle suotuisan pintalämpötilan tähden suhteen. Suoraan Stefan-Boltzmannin lain perusteella arvioitu planeetan pintalämpötila on $\sim \sqrt{(r_s/2R)}T_s$, missä $r_s$ on tähden säde, $R$ planeetan etäisyys tähdestä ja $T_s$ tähden pintalämpötila. Planeetan pintalämpötila ei riipu planeetan koosta, koska sekä tähdestä vastaanotettu (lisää energiaa) että ulospäin säteilty energia (vähentää energiaa) ovat molemmat verrannollisia planeetan säteen neliöön.

Huisaa miten sama fysiikan periaate toimii kahvikupista kosmisiin mittasuhteisiin! Mutta nyt keskustelu lähti hieman lapasesta. Jos palataan avaruudesta keittiöön, niin kuinka suuri säteilyteho kahvista sitten on?

Tehon laskemiseen emme voi käyttää Stefan-Boltzmannia yksipuolisesti, sillä lämpösäteilyn energiansiirtoon liittyy myös toinen puoli: kun kappaleen pinta säteilee lämpöä ympäristöön, myös ympäristö säteilee lämpöä kappaleeseen takaisin, samalla mekanismilla. Siten kahvin energiansiirto nettolämpösäteily on 

missä $T_{ympäristö}$ on ympäristön eli keittiön katon ja seinien absoluuttinen lämpötila. Näin ollen $60$-asteisen kahvin säteilemä teho kupin pinnalta $20$-asteisessa huoneessa on noin $\sim 1\; W$.

Nyt olemme tarkastelleet lämmönsiirtoa konvektiolla, johtumisella ja säteilemällä. Mutta entä se perustelu sille, että maito kannattaa lisätä heti kahvin kaadon jälkeen?

Tarkistetaan ensin, että olenko edes oikeassa. Eli tehdään koe.

Video 1: Kahvin lämpötila ajan funktiona kolmessa eri kokeessa: Ensimmäiseen kuppiin ei lisätä maitoa lainkaan, toiseen kuppiin lisätään maito reilu minuutti kaadon jälkeen, kolmanteen kuppiin reilu vartti myöhemmin. Lopputilanteessa lämpimämpää on maitokahvi, johon maito lisättiin aiemmin. Lisättävän maidon lämpötila ei riipu lisäämishetkestä.

Joo, uskotaan, eli maito tosiaan kannattaa kaataa kahviin myöhemmin. Mutta miksi?

Yllä havaitsimme, että kaikissa lämmönsiirtotavoissa teho kasvaa lämpötilaeron kasvaessa. Lämmönsiirtoteho mustaksi jääneestä kahvista on suurempi kuin maitokahvista; mustan kahvin sisäinen energia pienenee nopeammin kuin maitokahvin energia kahvin osalta (jos kahvia ja maitoa ajatellaan erillisinä komponentteina). Koska lisätyn maidon sisäinen energia on sama molemmissa tapauksissa, pidempään mustana pidetyn kahvin energia on pienempi ja lämpötila alempi myös maidon lisäämisen jälkeen.

Hmm, mutta toisaalta kahvin lämpötila pienenee enemmän tapauksessa, jossa maito lisätään aiemmin, kuumempaan kahviin.

Pohditaan hetkeä, jona maito kaadetaan kahviin. Ennen tätä hetkeä mitataan pelkkää kahvia, ja sen jälkeen kahvin ja maidon muodostamaa seosta. Kahvin lämpötila laskee, koska kahvi luovuttaa energiaa nimenomaan maidolle, sen lämpötilaa nostamalla. Kahvin lämpötila tosiaan laskee enemmän maitoa heti lisättäessä, mutta lämpötilan lasku kompensoituu vastaavalla nousulla maidon lämpötilassa.

Pitää sulatella, mutta eiköhän tämä perustelu jotenkin hahmotu. Mutta tuli vielä mieleen, että aiemmin kun esitit kaikenlaisia kaavoja, niin voiko kahvin lämpötilan myös ratkaista jotenkin matemaattisesti?

Kyllä voi. Ei kuitenkaan käydä mitään kaavasulkeisia, vaan otetaan napakasti. Lämpöä siirtyi kahvista konvektiolla, johtumalla ja säteilemällä, joten energiaa kahvista ympäristöön siirtyy yhteensä teholla $Q=Q_k+Q_j+Q_s$. Kahvin lämpötilan muutos $\Delta T_{kahvi}$ energian poistuessa riippuu puolestaan kahvin (veden) lämpökapasiteetista, eli $\Delta T_{kahvi}=\Delta E/m_{kahvi}c_v$, missä $\Delta T$ on kahvin lämpötilan muutos, $m_{kahvi}$ kahvin massa ja $c_v$ kahvin (eli veden) ominaislämpökapasiteetti. Kahvin energian muutos aikayksikössä on energian aikaderivaatta eli $d \Delta E/dt=Q$, mistä saadaan yhtälö kahvin lämpötilalle $T_{kahvi}$ ajan $t$ funktiona

Nyt menee aika heviksi…

No itsepä kysyit. Tämä kuitenkin on yhtälö, josta kahvin lämpötila voidaan ratkaista, tavalla tai toisella. Se on muodoltaan niin kutsuttu differentiaaliyhtälö, sillä se sisältää paitsi tuntemattoman ajan funktion $T_{kahvi}(t)$, myös funktion aikaderivaatan $dT_{kahvi}/dt$, joka siis myös on tuntematon. Tällaisia funktioita fysiikassa on paljon ja niiden ratkaisemiseen on olemassa erilaisia menetelmiä. Ehkä emme nyt kuitenkaan mene tässä tämän pidemmälle.

Ei mennä, ei. Mutta jos vielä yritän muotoilla tämän pointin itse, että ymmärsinkö oikein: kahvi pysyy kuumempana maiton aiemmin lisäämällä, sillä tällöin se on suurimman osan jäähtymisajasta viileämpää ja menettää siten vähemmän energiaa.

Juuri näin, hyvin kiteytetty!

Ja sama toisinpäin, eli mikäli haluaa nimenomaan välttää polttamasta kieltänsä, maito kannattaa lisätä juuri ennen juomista.

Niin, ja siinä tehokkainta lienee lisäksi pakotettu konvektio sekä puhaltamalla että lusikalla sekoittamalla.