Mikä siinä onkin, että kun puhelimen latausjohdon laittaa reppuun ja ottaa sen myöhemmin pois, niin johto on aina solmussa. Ja aina menee hetki aikaa johdon selvittämiseen. Ja auta armias jos repussa on kahden eri laitteen johdot… Joskus tuntuu, että johto haluaa mennä solmuun ihan kiusallaan.

Tilanne tosiaan on tuttu meille kaikille. Oletko joskus laittanut johdon reppuun ja ottanut sen välittömästi pois?

En muista… ehkä.

Joskus johto saattaa päätyä solmuun pelkästään kun sen laittaa pois ja ottaa jälleen käsiinsä. Tärkeää on siis myös se miten johtoon tarttuu kiinni. Saattaa nimittäin olla, ettei johto sinänsä ole solmussa — vaan sinä itse solmit sen johdon käteesi kun nykäiset sen esiin.

No joo, ehkä noinkin. Mutta ei repun pohjalla olevaa johtoa tule tutkittua sen tarkemmin.

No eipä varmaan. Ja tietenkin johdon höykytys repun pohjalla on jo sinänsä omiaan aiheuttamaan solmuja. Fysiikan kannalta tähän on selvä syy: johto menee solmuun, solmut saattavat johdon epäjärjestyneempään tilaan ja tämä kasvattaa johdon entropiaa.

Ja tämä liittyy siihen johonkin lakiin, jonka mukaan epäjärjestys kasvaa?

Kyllä, eli termodynamiikan toiseen pääsääntöön. Sen mukaan eristetyn systeemin entropia kasvaa tai pysyy samana, mutta ei koskaan vähene. Kuten rakkaalla lapsella on monta nimeä, tällä lailla on monia esitysmuotoja:

• Eristetyn systeemin kokonaisentropia kasvaa.

• Kaikki ajautuu järjestyksestä kaaokseen.

• Lämpö ei voi siirtyä kylmästä kappaleesta kuumaan kappaleeseen spontaanisti.

• Lämpöä ei voi muuttaa täydellisesti työksi.

• Eristetyn systeemin kappaleet ajautuvat aikaa myöten samaan lämpötilaan.

Video 1. Epäjärjestys kasvaa ajan myötä spontaanisti. Kun esimerkiksi ruokaa liikutetaan, usein sanotaan, että aineksia sekoitetaan, vaikka liikuttamisella ei varsinaisesti edes pyrkisi sekoittamiseen — sekoittuminen tapahtuu spontaanisti. Aineosien sekoittaminen järjestyneempään suuntaan puolestaan vaatii paljon aikaa ja työtä.

Tuon “kaikki ajautuu järjestyksestä kaaokseen” on kyllä helppo mieltää todeksi…

Joskus jopa maailman hullua menoa kuulee perusteltavan tällä fysiikan lailla. Termodynamiikan toista pääsääntöä ei kuitenkaan tule soveltaa epäjärjestykseen suoraan sellaisena kuin me ihmiset sen miellämme. Sotkuinen huone tai kaoottinen maailmanpolitiikka ei välttämättä ole lain tarkoittamaa epäjärjestystä. Termodynamiikassa epäjärjestys liittyy atomitason tapahtumiin, usein voimistuvan lämpöliikkeen mukanaan tuomaan epäjärjestykseen. Huolellisesti sovellettuna lain pohjalla olevalla periaatteella voi tosin perustella myös arkisia asioita.

Lakia voi käyttää jopa ajan suunnan määrittämiseen. Esimerkiksi Newtonin lait ovat ajan suunnan kääntämisen suhteen invariantteja. Aika eli parametri $t$ voidaan korvata $-t$:llä ja Newtonin lait toimivat edelleen. Tämä tarkoittaa, että biljardipelissä jokainen yksittäinen kimmoinen törmäys näyttäisi täysin luonnolliselta oikein- ja taaksepäin tarkasteltaessa eikä pelkästään niistä voisi päätellä ajan suuntaa. Ajan suunnan voi havaita, kun tarkastelee pallojen liikkumista kauemmin tai laajemmassa kontekstissa. Dissipatiivinen kitkavoima muuttaa mekaanista energiaa lämmöksi, mikä lisää mikroskooppista epäjärjestystä ja määrää ajan suunnan. Näyttäisi ilmeisen oudolta, mikäli paikallaan olevat biljardipallot lähtisivät levosta kiihtymään kohti toisiaan (saaden liike-energiaa palloihin juuri samaan suuntaan törmäilevistä ilman ja pöytäpinnan atomeista!), törmäilisivät toisiinsa, ja aiheuttaisivat lopuksi vain valkoisen pallon törmäämisen biljardikeppiin (Video 2).

Video 2: Ajan suunta määräytyy epäjärjestyksen kasvusta.

Ensinnäkin, mitä on “epäjärjestys”? Meidän täytyy ensin hahmottaa mitä fysiikassa tarkoitamme epäjärjestyksellä, jotta emme sekoita sitä arjen mielikuviin. Pyritään kuvaamaan epäjärjestystä objektiivisesti. Kuvaus onnistunee parhaiten esimerkillä.

Olkoon laatikossa 12 palloa. Palloista kuusi on sinistä ja kuusi punaista. Muuten pallot ovat täysin identtisiä. Järjestetään aluksi siniset pallot vasemmalle ja punaiset oikealle. Kuvataan tätä järjestynyttä tilaa tilamuuttujalla $n$, joka tässä olkoon vasemmalla olevien sinisten pallojen määrä. Alun järjestetyssä tilassa muuttujan arvo on $n=0$ (Kuva 2). 

Kun laatikkoa höykytellään, pallot pomppivat toistensa ylitse ja sekoittuvat. Ensimmäisen höykytyksen jälkeen $n=1$. Värit ovat hieman sekaisin, mutta tila näyttää vielä melko järjestyneeltä. Kun laatikkoa höykytetään toistamiseen, $n=1$. Kolmas höykytys antaa tilan $n=2$, neljäs höykytys tilan $n=3$, viides höykytys tilan $n=4$, ja kuudes höykytys tilan $n=3$ (Kuva 2).

Kuva 2. Laatikkoa höykytettäessä pallot sekoittuvat (nuolet). Tilamuuttuja $n$ kuvaa vasemmalla olevien sinisten pallojen määrää.

Jokainen höykytys on ikään kuin aikaa eteenpäin kuljettava kellon tikitys. Ajan edetessä pallojen värit menevät näennäisesti enemmän ja enemmän epäjärjestykseen. Epäjärjestyksessä sinisiä ja punaisia palloja on molemmin puolin suunnilleen yhtä paljon.

Nyt kuvittele seuraava tilanne. Pidät silmäsi kiinni sillä välin kun laatikkoa höykytetään hyvin pitkään. Tietyllä hetkellä avaat silmäsi ja katsot pallojen järjestystä. Nyt tulee keskeinen kysymys: Mitä luulet, mikä kuvassa 3 olevista tiloista näkisit todennäköisimmin? 

Kuva 2. Neljä erilaista järjestystä palloille.

Tämä on keskeinen kysymys, johon vastaus on, että kaikki järjestykset ovat täsmälleen yhtä todennäköisiä! Pallot olivat täysin identtisiä, joten pallojen toistensa lomitse pomppiminen on täysin riippumaton väristä.

Mutta eikö epäjärjestys ole kuitenkin todennäköisempi? Tuntuisi epätodennäköiseltä, että pitkän ajan kuluttua pallot olisivat maagisesti palanneet alkuperäiseen järjestykseen tai sen peilikuvaan. Epäjärjestyneet värit vaikuttaisivat todennäköisemmältä. 

Olet oikeilla jäljillä, mutta tässä on oltava tarkkana! Olennaista on huomata, että tarkastelemme kaikissa tapauksissa täsmällisiä, yksittäisiä järjestyksiä. Esimerkiksi järjestys B ei edusta monia epäjärjestyneitä tiloja — se edustaa vain ja ainoastaan itseään, tiettyä järjestystä, jossa pallot ovat täsmälleen kuvan järjestyksessä. Siitä huolimatta, että järjestys meidän silmäämme saattaakin vaikuttaa “geneeriseltä epäjärjestykseltä”. 

Aivan… Mutta näitä meidän silmäämme sekoittuneita järjestyksiä on enemmän!

Juuri niin! Tuo juuri on keskeinen oivallus. Laskeskellaanpa hieman erilaisten järjestysten lukumääriä, niin saamme käyttöömme konkreettisia lukuja.

Erilaisia järjestyksiä on yhteensä $12!/(6!\cdot 6!)=924$ kappaletta. (Eli kuinka monella tavoin voidaan järjestää $12$ palloa jaettuna kuinka monella tavoin voidaan järjestää $6$ sinistä ja $6$ punaista palloa keskenään. Pallothan ovat identtisiä, joten punaisten ja sinisten pallojen keskinäisellä järjestyksellä ei ole väliä.) Sellaisia järjestyksiä, joissa vasemmalla on $n$ sinistä palloa on yhteensä $\binom{6}{n}^2$ kappaletta. (Eli kuinka monella tavoin voit valita vasemmalta kuudesta paikasta $n$ sinistä paikkaa ja oikelta kuudesta paikasta $n$ punaista paikkaa, binomikertoimen avulla ilmaistuna.) Lasketaan näitä lukuja taulukkoon 1.

Taulukko 1. Tiettyä tilamuuttujan $n$ arvoa vastaava pallojen erilaisten järjestysten lukumäärä.

Kuvassa 2 olevan vaihtoehtojen B, C ja D tilamuuttujan arvo on $n=3$. Erilaisia järjestyksiä samalla tilamuuttujalla on $400$ kappaletta. Tällaisia $n=3$ tiloja on  $400/924=43$ % kaikista järjestyksistä. Kuvassa 2 olevan vaihtoehdon A tilamuuttujaa $n=0$ vastaa yksi ainoa järjestys. Tämä vastaa tuota sanomaasi lausahdusta “Epäjärjestyneet värit vaikuttaisivat todennäköisemmältä.” 

Ahaa! Eli “epäjärjestys” kuvaa jollakin tavoin järjestyksiä, joita yksinkertaisesti on paljon. 

Kyllä, juuri näin. Fysiikan suure tämän piirteen kuvaamiseen on entropia. Entropia on suuri tilanmuuttujien arvoilla, joita vastaa paljon yksittäisiä järjestyksiä. Tilamuuttujilla kuvataan systeemin makrotilaa eli jonkinlaista keskimääräistä ominaisuutta. Kuten meidän esimerkissämme $n$ eli sinisten pallojen määrä vasemmalla. Makrotilaa vastaa useita mikrotiloja, jotka puolestaan kuvaavat systeemin täsmällistä olotilaa (tässä pallojen täsmällinen  järjestys). Termodynamiikan toisen lain mukaan systeemi siis ajautuu kohti tilanmuuttujan arvoa (makrotilaa), jolla on suuri entropia eli jota voi kuvata suurella määrällä mikrotiloja. Epäjärjestys siis kasvaa siinä mielessä, että epäjärjestäytyneitä tiloja on aina suuri määrä ja niitä vastaavien makrotilojen entropia on suuri.

Tämä ehkä valaisi asiaa hieman… Mutta tarkennatko vielä, että mikä voima tai vastaava varsinaisesti ajaa kohti epäjärjestystä? 

Sepä siinä onkin: epäjärjestystä kohden ei aja mikään voima! Epäjärjestyminen ei ole mikään pyrkimys. Systeemi vain käy läpi (“sämplää”) pallojen järjestyksiä toinen toisensa perään. Pitkän ajan kuluessa kaikki järjestykset ovat yhtä todennäköisiä. Usein systeemit lähtevät kehittymään järjestyneestä tilasta, jonka entropia on pienempi. Siitä systeemit täysin luonnollisesti kehittyvät kohti epäjärjestystä — koska epäjärjestystä vastaa enemmän mikrotiloja. Myös ruoka sekoittuu kattilassa, vaikka et edes pyrkisi sekoittamaan eri ainesosia (Kuva 3).

Kuva 3. Aiemmassa videossa legot sekoittuivat ilman erillistä pyrkimystä. Sama pätee ruoka-aineisiin kokkaillessa.

Eli mahdollista on nähdä jossakin vaiheessa myös alkuperäinen, järjestynyt tila?

Kyllä, periaatteessa. Palloesimerkissä alkuperäinen tila $n=0$-tila voidaan havaita pitkän ajan kuluessa keskimäärin $1/924=0{,}11$ %:n todennäköisyydellä. Pienissä systeemeissä kuten tässä tapahtuu paljon fluktuaatioita, eli tilamuuttujan vaihteiluita. Mikrotilojen määrä ja fluktuaatiot kuitenkin pienenevät voimakkaasti systeemin koon kasvaessa. Jos palloja olisi sata, eli $50$ sinistä ja $50$ punaista palloa, niin erilaisia järjestyksiä olisi jo $1{,}0\times 10^{29}$ kappaletta! Näin monella pallolla et todennäköisesti päätyisi alun järjestettyyn tilaan edes maailmankaikkeuden iän aikaskaalassa, ei vaikka laatikkoa höykytettäisiin kerran nanosekunnissa. Voimme vain kuvitella mikrotilojen lukumäärien suuruusluokkia atomistisissa systeemeissä, joissa hiukkasia on Avogadron vakion $6{,}022\times 10^{23}$ verran.

Emme kuvaa systeemin entropiaa $S$ tässä nyt kvantitatiivisesti, mutta karkeasti kuvattuna se on verrannollinen mikrotilojen lukumäärän $N$ logaritmiin, $S\propto \log N$. Laatikon kaltainen eristetty systeemi on tasapainossa, kun tilamuuttujaa vastaava entropia $S$ on maksimissaan eli se ei voi enää kasvaa.

Entä miten tämä kaikki liittyy solmuisiin johtoihin?

Yllä katsoimme yleisiä periaatteita epäjärjestykselle, entropialle ja sen kasvamiselle. Taipumusta mennä solmuun voidaan ymmärtää samojen periaatteiden avulla. Solmuun menoa olisi erittäin vaikea tarkastella kvantitatiiviseti, mutta pyritään rakentamaan ilmiölle edes laadullinen ymmärrys.

Värikkäiden pallojen sijasta meillä on siis johto, jota voidaan kuvata tietyn mittaisena, taipuisana, elastisena lankana. Johdon (mikro)tilaa kuvaa sen päiden etäisyys toisistaan sekä sen välissä oleva täsmällinen muoto. Solmuttomalla johdolla on numeroimattoman monta tapaa olla mutkalla. Muoto voi jopa leikata itsensä, mutta ehtona on, että mutkaisuus ei vastaa topologisesti solmua (Kuva 4). Solmullisella johdolla on myös numeroimattoman monta tapaa olla mutkalla — keskeisenä erona on se, että muodolle ei ole topologista rajoitetta. 

Solmuisella johdolla on siten suoraa johtoa paljon (!) enemmän tapoja olla mutkalla. Toisin sanoen, solmuisella johdolla mikrotiloja on enemmän (vaikka johdon tapauksessa emme niitä voikaan yksilöidä). Johdot päätyvät solmuun, koska solmuisan johdon entropia on suuri.

Mikäli entropian kasvua johdon tapauksessa on vaikea hahmottaa, pohdi seuraavaa tilannetta. Metrin pituisella johdolla on tietty, numeroimattoman suuri määrä tapoja olla mutkalla. Yksi solmu lyhentää johtoa suhteessa vähän, vaikkapa viisi senttiä. Jäljelle jääneellä $95$ cm:n johdolla on edelleen lähes yhtä monta tapaa olla mutkalla kuin alkuperäisellä metrin johdolla. Mutta sen lisäksi solmu voi sijaita missä kohdassa johtoa tahansa (Kuva 4). Siten lienee uskottavaa, että jo yhden solmun johdolla on solmutonta johtoa suurempi entropia. Tämän lisäksi “solmussa olevassa johdossa” voi olla useampi kuin yksi solmu. Ja solmujakin voi olla monenlaisia.

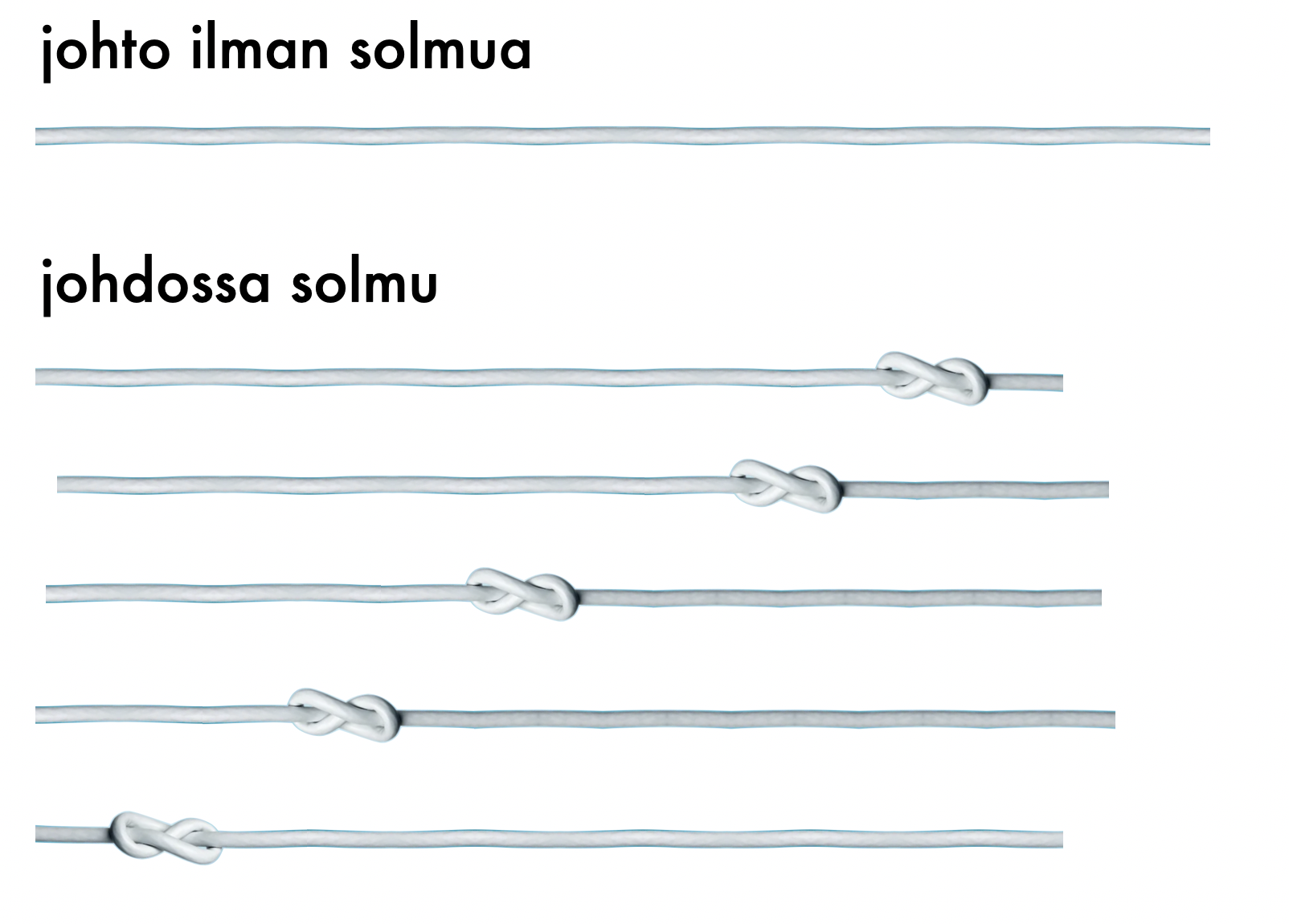
Kuva 4. Solmu voi sijaita eri kohdassa johtoa. Lisäksi johto voi olla mutkalla monin eri tavoin.

Mutta usein johdoissa on vain solmu tai kaksi. 

Minulla on sama havainto. Solmujen vähyys liittyy osin asiaan, jota pallojen tapauksessa ei tullut esiin ja jota emme ole vielä ottaneet huomioon: solmut myös maksavat energiaa. Johto on elastinen lanka, joka vastustaa taipumista, joten solmiminen edellyttää työn tekemistä; energeettisesti johto haluaisi olla suorassa. Tämä tarkoittaa, että systeemi ei pelkästään pyri entropian maksimoimiseen, vaan myös energian minimoimiseen. Elastinen energia pyrkii pitämään johdon suorassa, entropian kasvu ajaa johtoa solmuun. Energia ja entropia kilpailevat keskenään. 

Termodynamiikassa tätä kilpailua voidaan kuvata vapaalla energialla 

missä $E$ on systeemin elastinen energia, $T$ on absoluuttinen lämpötila ja $S$ entropia. 

Eli lämpötila T tuossa on huoneenlämpötila vai mikä?

Ei, vaan puhumme nyt lämpötilasta ainoastaan laadullisella tasolla. Johdon tapauksessa lämpötilan $T$ voi ajatella vastaavan johdon höykyttelyn määrää repun sisällä. “Kylmä” tarkoittaa paikallaan olevaa reppua ja johdon vähäistä häiritsemistä, “kuuma” tarkoittaa repun reipasta höykyttelyä ja johdon sekoittelua. Kun höykytystä on vähän (pieni $T$), elastinen energia pyrkii pitämään johdon suorassa ja johto sämplää enimmäkseen matalan energian (suoria) muotoja. Kun höykytystä on paljon (iso $T$), elastinen energia on pieni verrattuna höykytyksen suureen määrään ja johto sämplää kaikenlaisia muotoja — ja koska solmuisia muotoja on enemmän, johto päätyy todennäköisesti solmuun. 

Tätä keskustelua ei kannata ottaa liian tarkasti, sillä kyse on laadullisista ideoista. Solmuun menoa voi siis kuitenkin yrittää välttää jäykillä johdoilla (iso elastinen energia) ja vähällä höykytyksellä (vähentää entropian merkitystä). Nämä johtopäätökset ovat toki intuitiivisesti ilmeisiä, tällä tavoin voi hahmottaa myös fysiikan periaatteita ilmiön takana. Huomiota voi silti kiinnittää myös siihen miten johtoon tarttuu sitä pois ottaessa. Ettei johtoa vahingossa tule laitettua solmuun itse!