Miten tietokonepelit mallintavat fysiikkaa?
Tietokonepelit mallintavat nykyään fysiikkaa melko tarkasti. Voiko niiden avulla tutkia myös arjen fysiikan ilmiöitä?
Ilmiöiden tutkimiseen tietokonepelit soveltuvat kyseenalaisesti — etenkin jos tutkittava asia on pelin fokuksen ulkopuolella. Yleensä pelejä ei ole tehty opettamaan fysiikkaa, vaan viihdyttämään (tai paremmin: myymään). Peleissä on juuri sen verran fysiikkaa kuin sitä niihin on ohjelmoitu. Aina pelien ilmiöt eivät edes perustu varsinaisiin fysiikan malleihin, vaan helposti ja nopeasti ohjelmoitaviin malleihin, jonkinlaiseen näennäisfysiikkaan, jota on myös nopea laskea.

Kuva 1: Fysiikkaa mallinnettiin Grand Prix Circuit -pelissä (1988) melko rajoitetusti.
No joo, pelit aikanaan nyt olivat mitä olivat. Mutta nykyään pelien ilmiöt ja liikkeet kyllä nykyään vaikuttavat hyvinkin realistisilta. Ne noudattavat ainakin omia intuitioita monista ilmioistä.
Ehkä joissakin tapauksissa. Laskentatehon kasvu on tehnyt peleistä näennäisesti realistisia, mutta realistisuus on usein pinnallista. Pelien kehittäjienkin tavoitteissa saada pelin maailma tuntumaan todelta. Kuitenkin pelien ilmiöt ovat usein äärimmäisiä suhteessa arjen kokemuksiin. Harvalla meistä on kokemusta vaikkapa ajamisesta autolla  ,
,  :n kiihtymisestä avaruusraketissa, tai pomppimisesta vieraalla planeetalla, jonka vieressä on musta aukko. Esimerkiksi usein pelien avaruusalukset lentävät usein kuin lentokoneet.
:n kiihtymisestä avaruusraketissa, tai pomppimisesta vieraalla planeetalla, jonka vieressä on musta aukko. Esimerkiksi usein pelien avaruusalukset lentävät usein kuin lentokoneet.
Miksi niin?
Luulisin, että syynä on se, että tunnemme itse kohtalaisesti lentokoneiden lentämiseen liittyvät seikat kuten sen että lentokoneen nokka osoittaa liikkeen suuntaan. Todellisuudessahan avaruusaluksilla nokka voisi osoittaa mihin suuntaan vain ja alusten pysäyttäminen kestäisi usein yhtä kauan kun niiden kiihdyttäminen. Poikkeuksia peleissä toki on. Vaikkapa Kerbal Space Program -pelissä idea on juuri mallintaa realistisia avaruusaluksia.
Mutta yleisesti peleissä joitakin ilmiöitä saatetaan muokata viihdyttävämpään ja samalla epärealistisempaan suuntaan. Silti pelin tekijän on osattava fysiikkaa hyvin, jotta osaa tehdä hyvän pelin. Liika epärealistisuus saattaa tehdä pelimaailmasta vähemmän samaistuttavan. Henkilöstä ei voi tulla hyvää asianajajaa, ellei tunne lakia. Fysiikan osaamisen vaade pätee myös elokuvien tekoon erikoistehosteiden kautta.
Mutta fyysikko ei ole automaattisesti hyvä pelintekijä.
Joo, ei toki automaattisesti. Fysiikan lakien soveltaminen peleissä on oma taiteenlajinsa. Ja väistämättä jossakin vaiheessa pelin tekijän on luovuttava fysiikan täsmällisestä oikeellisuudesta rajallisen laskentatehon vuoksi.
Mitä pelifysiikka sitten on, miten sitä koodaillaan?
Pelien fysiikka on pitkälti klassista mekaniikkaa, jossa pistemäiset, jäykät tai pehmeät kappaleet törmäilevät ympäristöön ja toisiinsa. Pelifysiikan tarkoitus on simuloida reaalimaailman tilanteita mahdollisimman hyvin, jotta pelaaja pystyisi samaistumaan pelin maailmaan ja uppoutumaan siihen entistä paremmin.
Ehkä keskeisin piirre fysiikan ohjelmoinnissa on tämä: tietokoneella kaikki fysiikka mallinnetaan diskreettien suureiden avulla. Mikään suure ei ole jatkuva ajan eikä paikan suhteen. Nykyään pelejä tehdään fysiikkamoottoreilla, jotka huolehtivat kappaleiden dynamiikasta ja kinematiikasta melko automaattisesti.
Mitä olivatkaan dynamiikka ja kinematiikka?
Dynamiikassa tarkastellaan sitä miten voimat vaikuttavat kappaleen liikkeeseen. Dynamiikan perusta on Newtonin toinen laki  , jonka mukaan kappaleen kiihtyvyys
, jonka mukaan kappaleen kiihtyvyys  aiheutuu siihen kohdistuvasta kokonaisvoimasta
aiheutuu siihen kohdistuvasta kokonaisvoimasta  ja on kääntäen verrannollinen kappaleen massaan
ja on kääntäen verrannollinen kappaleen massaan  . Kinematiikka puolestaan keskittyy kappaleen liikkeen kuvailuun ja kertoo vaikkapa millaista on tasainen liike, tasaisesti kiihtyvä liike, tasainen pyörimisliike, tai tasaisesti kiihtyvä pyörimisliike. Esimerkiksi
. Kinematiikka puolestaan keskittyy kappaleen liikkeen kuvailuun ja kertoo vaikkapa millaista on tasainen liike, tasaisesti kiihtyvä liike, tasainen pyörimisliike, tai tasaisesti kiihtyvä pyörimisliike. Esimerkiksi  :n ollessa vakio kappale kiihtyy tasaisesti ja liikettä voidaan kuvata tietyillä kaavoilla. Kinematiikka tarkastelee miten kappale liikkuu, dynamiikka tarkastelee miksi liike on sellaista kun se on.
:n ollessa vakio kappale kiihtyy tasaisesti ja liikettä voidaan kuvata tietyillä kaavoilla. Kinematiikka tarkastelee miten kappale liikkuu, dynamiikka tarkastelee miksi liike on sellaista kun se on.
Olisiko mahdollista käydä läpi fysiikan koodaamista jonkin esimerkin avulla?
Jo vain. Fysiikkamoottoreistakin on enemmän huvia ja hyötyä, kun on käsitys siitä mitä moottorit pitävät sisällään. Otetaan tarkasteluun esimerkiksi tyypillisiä heitto- tai pallottelupelin ilmiöitä, joissa tulee vastaan pelien perusmekaniikkaa.
Lähdetään siis liikkeelle ja edetään vaiheittain. Esitetään lausekkeita pseudokoodilla, jotta ohjelmointinäkökulma tulee esille selvemmin.
Oletetaan pelissä mallinnettavaksi esineeksi jäykkä, pyöreä kappale, jonka säde on r ja massa m (Kuva 2). Ajanhetkellä i kappaleen paikka on (x[i], y[i]) ja nopeus on (v_x[i],v_y[i]) missä i on diskreettejä ajanhetkiä indeksoiva kokonaisluku.
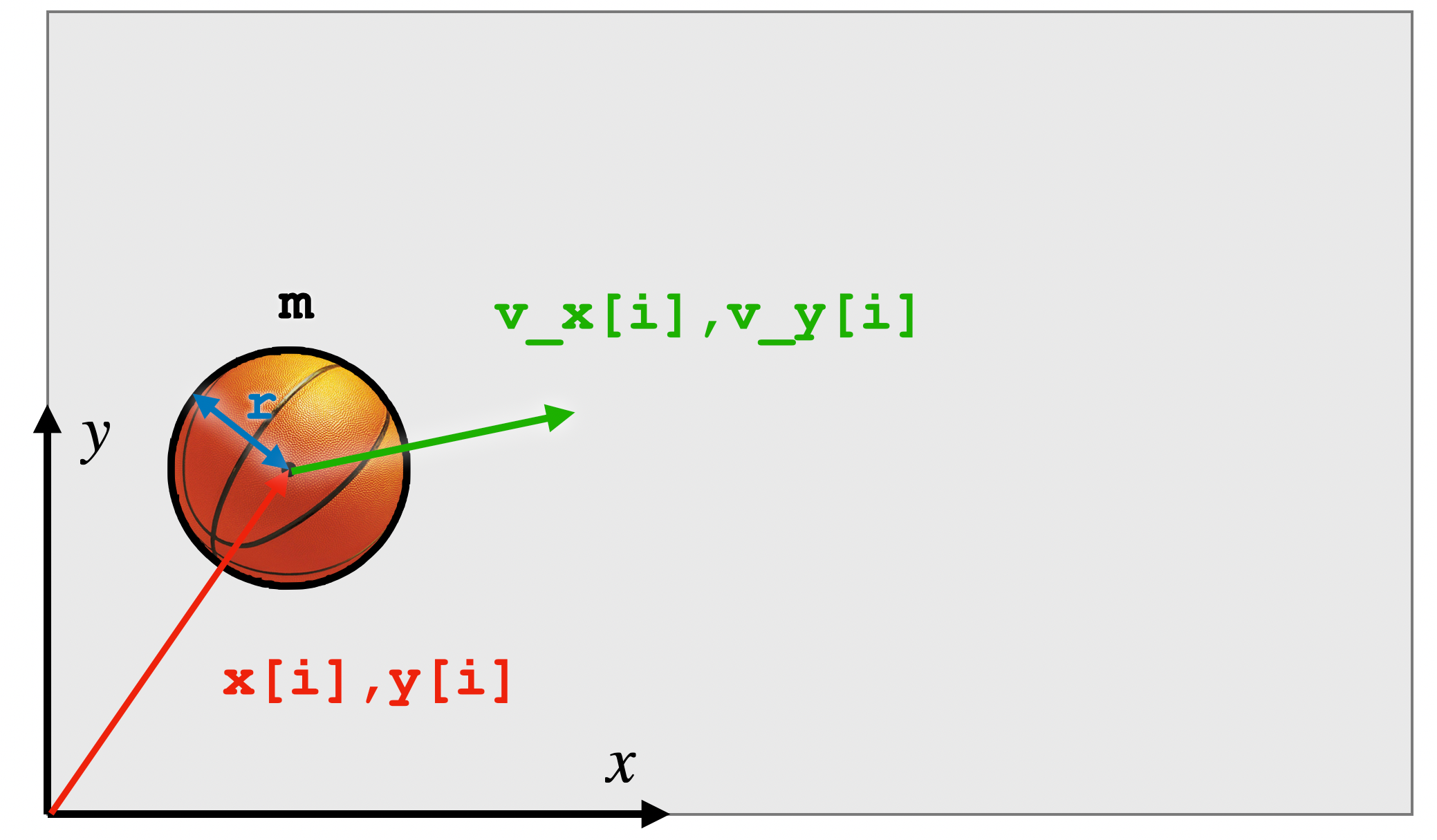
Kuva 1. Ajanhetkellä i kappale on paikassa (x[i],y[i]) ja liikkuu ruudulla hetkellisesti nopeudella (v_x[i],v_y[i]) (esimerkiksi yksiköissä pikseliä per aika-askel).
Mikäli kappaleeseen vaikuttavien voimien summa on nolla, Newtonin I lain mukaan se säilyy levossa tai jatkaa tasaista liikettä nopeudella (v_x[i],v_y[i]). Tällöin kappaleen paikka seuraavalla ajanhetkellä i+1 on
x[i+1] = x[i]+v_x[i]*dt ja
y[i+1] = y[i]+v_y[i]*dt,
missä hetkien i ja i+1 välissä on kulunut lyhyt aika dt. Pallon heitossa aikaväli voisi olla esimerkiksi dt=0.01 sekuntia, jolloin pallon liike animoituna näyttäisi omiin silmiimme jatkuvalta.
Jos kappaleeseen vaikuttaa kokonaisvoima  , kappaleen nopeus muuttuu Newtonin toisen lain
, kappaleen nopeus muuttuu Newtonin toisen lain
määräämän kiihtyvyyden vuoksi. Tällöin ajanhetkellä i+1 kappaleen x-suuntainen nopeus on
v_x[i+1]=v_x[i] + a_x[i]*dt (1)
ja x-koordinaatti on
x[i+1]=x[i]+v_x[i]*dt + 1/2*a_x[i]*dt**2. (2)
Nopeus ja paikka y-suuntaan lasketaan samalla tavalla.
Nuo kaavat näyttävät tutuilta.
Ne ovatkin fysiikan oppikirjoista tuttuja kinematiikan peruskaavoja tilanteissa, joissa kiihtyvyys on vakio. Ja vaikka (voiman muuttuessa) kiihtyvyys muuttuisikin, kaavoja voi käyttää kohtuullisella tarkkuudella, kunhan aikaväli dt on riittävän pieni, eli kiihtyvyys muuttuu aikavälillä dt riittävän vähän eli on suunnilleen vakio.
Mikä on riittävän vähän?
Se riippuu aina tilanteen monimutkaisuudesta ja tavoiteltavasta tarkkuudesta. Koodatessa on onneksi helppo testailla erilaisia parametreja ja tarkastella niiden vaikutusta lopputulokseen.
Erilaisten voimien ja vuorovaikutusten lisääminen malliin onkin sitten varsin suoraviivaista. Jos kappaleeseen kohdistuu pelkästään painovoima alaspäin eli -y-suuntaan, niin a_y=-g aina. Analyyttisesti haastavan ilmanvastusvoiman lisääminen on yhtä suoraviivaista, ainoastaan lauseke on pidempi. Kurssin johdantokappaleessa tulikin esille, että ilmanvastusvoimalle on olemassa malli
Tällöin ilmanvastusvoima voidaan mallintaa lisäämällä kiihtyvyyteen termi
a_x =a_x - b*v_x[i]/(v_x[i]**2+v_y[i]**2)**(3/2)/m
x-suuntaan ja samoin y-suuntaan. Näin esimerkiksi painovoimakentässä vapaasti liikkuvaa palloa ilmanvastuksella voi mallintaa kiihtyvyyksillä
a_x[i]=-b*v_x[i]/(v_x[i]**2 + v_y[i]**2 )**(3/2)/m
a_y[i]=-g-b*v_y[i]/(v_x[i]**2+v_y[i]**2)**(3/2)/m
ja soveltamalla kaavoja (1) ja (2) yllä suoraan.
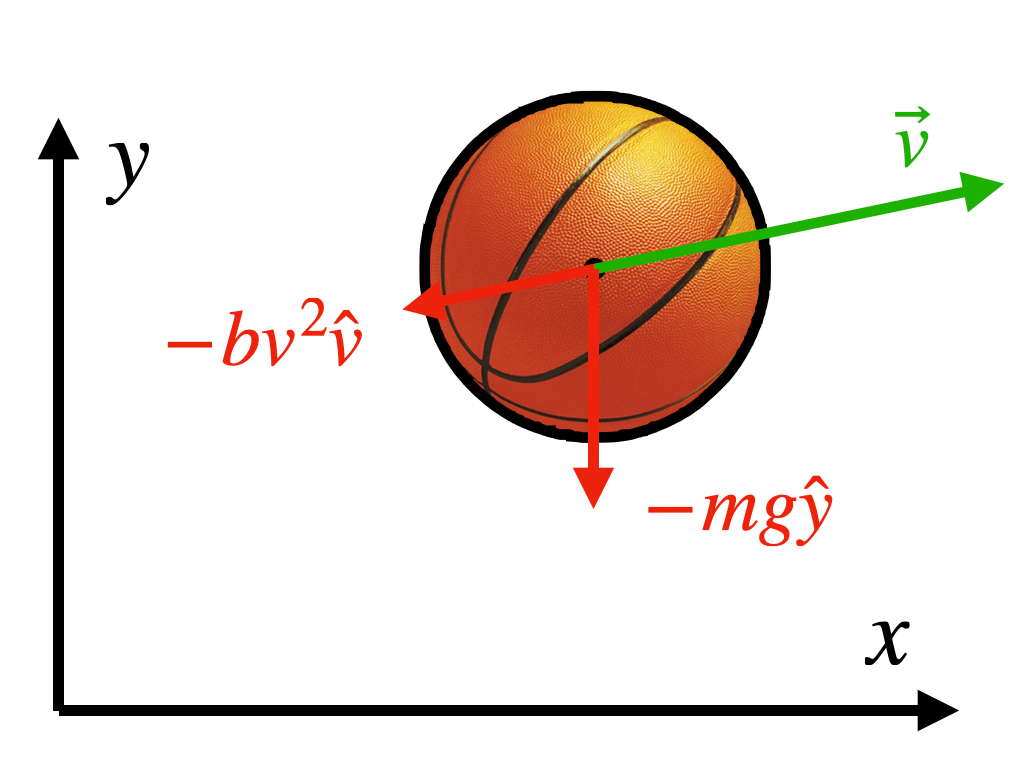
Kuva 3. Kappaleeseen kohdistuu painovoima ja nopeudesta riippuva ilmanvastus.  merkitsee
merkitsee  :n suuntaista yksikkövektoria.
:n suuntaista yksikkövektoria.
Samaan tyylin voisimme lisätä minkä tahansa kappaleeseen kohdistuvan voiman. Nopeus ja paikka seuraavalla aika-askeleella laskettaisiin täsmälleen samalla tavalla. Kaikenlaisten voimien lisääminen on periaatteessa yhtä suoraviivaista; tämä osoittaa numeerisen laskennan hyödyn. Jos kappaletta vaikka ohjattaisiin näppäimistöllä, niin kiihtyvyyksiin voisi lisätä termit
a_x[i] += Fx
a_y[i] += Fy
missä Fx ja Fy ovat hetkellisiä voimia, jotka syntyvät vaaka- tai pystysuuntaisten nuolinäppäinten painalluksista.
Entä sitten törmäykset sun muut?
Törmäykset etenkin vaaka- ja pystysuoriin pintoihin ovat nopeita mallintaa. Esimerkiksi, jos laskemme kappaleen korkeuden y[i+1] ajanhetkellä i ja toteamme sen olevan liian matalalla (y[i+1]<r), voimme tulkita kappaleen törmäävän hetkien i ja i+1 välillä maahan. Voimme tällöin suoraan vaihtaa nopeuden pystysuoran komponentin etumerkin
v_y[i+1] = -v_y[i],
ja (vaakasuuntaisten voimien puuttuessa) pitää vaakasuuntaisen nopeuden vakiona,
v_x[i+1] = v_x[i].
Koordinaatteja voidaan approksimoida esimerkiksi tyyliin x[i+1]=x[i]+v_x[i]*dt ja y[i+1]=y[i]. Tämä approksimaatio vastaa täysin elastista törmäystä maahan. Jälkimmäinen lauseke olettaa, että törmäys tapahtuisi juuri aika-askeleiden puolivälissä, eikä siten ole aina oikein. Mutta mikäli dt on pieni, virhekin on pieni.
Mikä olikaan elastinen törmäys?
Elastisessa törmäyksessä liike-energia säilyy ja energiaa ei muutu lainkaan lämmöksi. Epäeläastisessa törmäyksessä osa liike-energiasta muuttuu lämmöksi, jolloin törmäävien kappaleiden liike-energia pienenee. Epäelastisuutta voi kuvata kimmoisuusasteella e, joka kertoo kuinka paljon kappaleen nopeus törmäyksessä pienenee. Voisimme mallintaa edellä esitetyn törmäyksen epäelastisena, mikäli pystysuora nopeus pienenee (v_y[i+1] = -e*v_y[i]) samalla kun pinnan suuntainen nopeus säilyy (v_x[i+1] = v_x[i]).
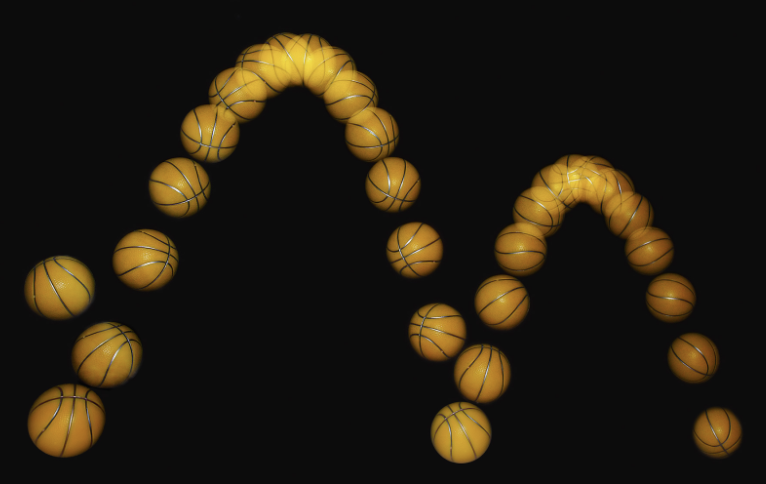
Kuva 4. Epäelastisissa törmäyksissä maahan mekaaninen energia pienenee.
Jäin miettimään, että menikö tuo törmäys yllä ihan oikein…?
Tarkasti ottaen ei. Jo näin yksinkertaisissa törmäyksissä tulee esiin ajan diskreettisyys tuo haasteita koodaamiseen: törmäys maahan tapahtuu jossakin aikavälien i ja i+1 välillä, mutta emme täsmälleen tiedä milloin. Voisimme kyllä ratkaista sen, mutta on paljon helpompaa vain kääntää pystysuora nopeus ja jättää huomiotta se, että kappaleen dynamiikka tulee laskettua hieman väärin. Mitä pienempi on aikavälin pituus dt, sitä pienempi on tästä aiheutunut virhe.
Lisäksi joudumme törmäyksen yhteydessä tekemään päätöksiä fysiikan mallinnuksen tasosta. Haluammeko törmäysten olevan elastisia vai epäelastisia? Jos seinämme onkin liikkuva taso (kuten maila), voiko tason liikkeellä vaikuttaa kappaleen liikkeeseen tason suuntaan? Vai voiko pinta muuttaa kappaleen liikettä vain pinnan normaalin suuntaan? Ja riittääkö yleensäkään, että mallinnamme kappaletta pisteenä (joka ei lähtökohtaisesti voi pyöriä)? Onko olennaista, että pyöriminen huomioidaan, jolloin pinnan suuntainen liike törmäyksessä aiheuttaisi myös vääntömomentteja? Riittääkö liikkeen suuntainen ilmanvastus, vain voiko pyöriminen aiheuttaa myös Magnus-efektin? (Magnus-efektiä tarkastelemme jalkapalloon liittyvässä osiossa).
Koodareina joudumme usein pohtimaan kumpi on tärkeämpää: koodin tehokkuus vai fysiikan tarkkuus. Periaatteessa kaiken voisi jättää Newtonin lakien ja (erittäin) pienen aika-askeleen huoleksi, mutta koodista tulisi tehotonta.

Kuva 5. Jos nopeus  tai aika-askel
tai aika-askel dt ovat toistensa suhteen liian suuria, kappaleet saattavat mennä hetkeksi toistensa “sisään” (kuten tässä pallo lattian sisään), mikä voi johtaa pelin jumiutumiseen.
Entä kappaleiden törmäykset toisiinsa?
Jo kahden pyöreän kappaleen toisiinsa törmäämisen mallintaminen menee yllättävän sotkuiseksi. Energian ja liikemäärän säilymislakien avulla on kuitenkin mahdollista johtaa lausekkeet kappaleiden uusille nopeuksille törmäyksen jälkeen.
Eikö tässä tarvita myös Newtonin kolmatta lakia? Eli sitä jonka mukaan kappaleiden toisiinsa kohdistamat voimat ovat yhtä suuret ja vastakkaissuuntaiset?
Tavallaan kyllä, mutta ei erikseen, sillä Newtonin kolmas laki on jo periaatteellinen syy liikemäärän säilymiseen törmäyksissä. Törmäysten mallintamisessa ei kuitenkaan ole välttämätöntä käyttää voimia lainkaan; säilymislait ovat mallintamisessa paljon tehokkampia (jokin suure ennen ja jälkeen törmäyksen on sama). Jäykille kappaleille voimien käyttäminen ei ole edes mahdollista, sillä törmäysten kestot käytännön tilanteissa mitataan millisekunneissa ja sitä lyhyemmissä aikaväleissä; niitä ei siten voi mallintaa samalla aika-askeleella dt, jota käytetään liikkeen kuvaamiseen suuremmissa pituusskaaloissa ja pidemmissä aikaskaaloissa.
Entä sitten jos tuo pallo osuu maahan vinottain ja alkaa pyöriä?
Tämä kysymys liittyy edellä pohtimaamme fysiikan mallintamiseen. Esimerkissämme meillä on jäykkä kappale, jolla on tietty koko, mutta joka muuten on pistemäinen (kaikki massa kappaleen keskipisteessä). Pistemäisenä mallinnettu kappale ei voi pyöriä; kappaleen paikka ja nopeus kertovat kappaleesta kaiken mahdollisen. Pyörimistä varten meidän tulisi mallintaa jäykkiä kappaleita, joiden massa on jakautunut esimerkiksi homogeenisesti. Ja törmäyksissä pitäisi sallia vieläpä pintojen suuntaiset kitkavoimat. Mielivaltaisten muotoisten jäykkien kappaleiden törmäysten tietokoneelle ohjelmoitavat kaavat olisivat siten erittäin (!) sotkuisia.
Joissakin tapauksissa saattaa olla helpompaa, mikäli jäykkien kappaleiden sijaan mallinnetaan pehmeitä kappaleita, joissa voi tapahtua myös muodonmuutoksia. Pehmeitä kappaleita voi mallintaa esimerkiksi pistejoukolla, joka on kytketty toisiinsa jousilla (Video 1). Tällöin kappaleen jokaiselle pisteelle lasketaan paikka ja nopeus erillisenä pistemäisenä kappaleena; pistejoukon muoto ja sijainti sitten kuvaa koko pehmeän kappaleen käyttäytymistä.
Video 1: Karkea pehmeän kappaleen malli koripallosta. Kappale koostuu 21 erillisestä massapisteestä, jotka on yhdistetty toisiinsa jousilla ristiin rastiin. Pallon liikkuminen, törmääminen ja pyöriminen syntyvät yksittäisten pisteiden erillisestä dynamiikasta.
Kaikkiaan törmäykset ovat peleissä tärkeitä, sillä usein pelihahmojen liikkuminen perustuu törmäyksiin; jo pelkkä kävely on jalkojen “törmäilyä” maahan.
Missä vaiheessa keskustelemme niistä fysiikkamoottoreista?
Keskustelemme niistä periaatteessa koko ajan. Nykyään fysiikkaa kun harvoin enää ohjelmoidaan jokaiselle kappaleelle erikseen kuten koodinpätkillä yllä. Sen sijaan hyödynnetään fysiikkamoottoreja, jotka huolehtivat fysiikan simuloinnista pelimaailmassa. Se luo peliin fysiikan lakien mukaisen ympäristön, jossa esineet ja hahmot liikkuvat, vuorovaikuttavat ja reagoivat toisiinsa ja ympäristöön. Fysiikkamoottorit ilmentävätkin fysiikan kauneutta: samat lait pätevät kaikille kappaleille kaikissa tilanteissa, mallinnuksen tasosta riippuen.
Fysiikkamoottorit hallitsevat useita fysiikan osa-alueita, kuten
-
kappaleiden liikettä,
-
törmäyksiä,
-
kontaktivoimia,
-
painovoimaa,
-
vastusvoimia (kitka ja ilmanvastus),
-
räjähdyksiä,
-
virtausmekaniikkaa,
-
muodonmuutoksia,
-
optiikkaa
ja monia muita ilmiöitä. Lisäksi moottori ottaa tietenkin huomioon pelaajan hiiren liikkeet ja nappien painallukset tarpeen mukaan. Moottorien avulla pelintekijät voivatkin keskittyä kehittämään pelin ideaa, grafiikkaa ja muuta pelille ominaista piirrettä. Moottorien kautta fysiikkaa voi ottaa mukaan sen verran kuin on tarve (Video 2).
Video 2. Kappaleen putoaminen kaltevalla tasolla, fysiikkamoottorin neljällä tasolla mallinnettuna. 1) Ei fysiikkaa, 2) painovoima ilman törmäysten tunnistamista, 3) painovoima ja törmäysten tunnistaminen, mutta ilman jäykän kappaleen mekaniikka ja 4) painovoima, törmäysten tunnistaminen ja jäykän kappaleen pyörimisliike (Wikimedia Commons).
Mutta entä sitten alkuperäinen kysymys? Jos pelit on rakennettu fysiikkamoottorien avulla, niin eikö peleillä sitten voisi tutkia arjen fysiikan ilmiöitä? Jos käyttää fysiikkamoottoria tarkimmilla mahdollisilla säädöillä.
Tutkiminen on aika voimakas sana tässä yhteydessä. On totta, että fysiikka monissa nykyajan peleissä on tarkasti mallinnettu, mutta tarkemmin katsoessa realistisuudessa on aina tingitty jossakin vaiheessa. Ehkä voisi muotoilla vastauksen siten, että tietyn ilmiön tutkiminen on mahdollista, mikäli tuntee fysiikkamoottorin toiminnan tarpeeksi hyvin juuri kyseisen ilmiön suhteen.
Oma lukunsa on fysiikan simulaatio-ohjelmat, joita ei toki ole rakennettu peleiksi, vaan tietynlaisen fysiikan mallintamiseen. Ohjelmistoja löytyy jokaiseen ilmiöön kappaleiden mekaniikasta (FEM-mallinnus) atomistiseen ja kvanttimekaaniseen molekyylidynamiikkasimulaattoriin. Näissä ohjelmissa fysiikan tarkkuudesta tingitään harvoin; esimerkiksi pienen molekyylin ominaisuuksien laskemiseen yhdellä ainoalla geometrialla saattaa mennä vuorokausi supertietokoneella. Ohessa Jyväskylän yliopiston fysiikan laitoksen professori Ilari Maasilta kertoo simuloinnista fysiikan tutkimuksessa (Video 3).
Video 3: Professori Ilari Maasilta kertoo miten ilmiöiden simulointi tukee kokeellisen fysiikan tutkimusta.
Hauskoja mutta erityisen hyödyllisiä ovat ohjelmat pelien ja fysiikan simulaatio-ohjelmien välimaastosta. Ne kuvaavat haluttua fysiikan ilmiötä kohtuullisen hyvin, mutta ovat myös viihdyttäviä. Esimerkki tällaisesta ohjelmasta on Algodoo, jota on hyötynnetty myös tällä kurssilla (esimerkiksi Video 1 yllä on tehty Algodoolla). Myös laajasti hyödynnetyt PhET-simulaatiot voidaan laskea mukaan tähän kategoriaan.
Peleissä tärkeää on myös näyttävät grafiikat. Oman kategoriansa muodostavatkin säteenseurantaohjelmat, jotka pyrkivät mallintamaan optista fysiikkaa mahdollisimman tarkasti, ja joilla voi laatia fotorealistisia kuvia pelimaailman objekteista. Näistä riittäisi juttua omaan osioonsa, joten ei mennä niihin sen syvemmälle.
Jos minua kiinnostaisi kokeilla jonkin yksinkertaisen pelin tekemistä fysiikkamoottorin avulla, mistä voisin lähteä liikkeelle?
Pelimoottoreita on tarjolla moneen lähtöön: Pygame, The Unreal Engine, Unity, Godot,... Mutta, kuten edellä mainitsin, fysiikka kannattaa hallita myös itse — älä jätä sitä pelkästään moottoreiden varaan!
| Tiivistelmä |
| Tietokonepelien fysiikka eroaa usein tarkoituksella tosielämästä. |
| Tietokonepeleissä kaikki fysiikka mallinnetaan diskreettien muuttujien avulla. |
| Tietokoneohjelmissa liike ei ole täysin jatkuvaa vain koostuu tiuhaan toistuvista yksittäisistä tilanteista. |
| Fysiikan mallintamisessa pitää tehdä valintoja laskukyvyn ja tarkkuuden välillä. |

