Kvanttimekaniikkaa ja suhteellisuusteoriaa yleissivistävästi
Section outline
-

Kysymyksessä Miten hiukkanen voi olla samaan aikaan kahdessa eri paikassa? kaksoisrakokokeen yhteydessä tosiaan mainittiin kvanttimekaaninen ilmiö tunneloituminen. Termi saattaa olla tuttu muualtakin. Hiukkasen tunneloitumisessa on kyse siitä, että kvanttimekaanisesti hiukkanen tosiaan läpäisee esteitä tavalla, joka klassisesti on mahdotonta.
Mutta että seinän lävitse, ei kai nyt sentään…?
No, se riippuu toki seinästä ja hiukkasesta. Mutta tutkitaan mistä on kyse.
Jatketaan niistä lähtökohdista, joihin päädyimme kysymyksessä Onko kvanttimekaniikassa vastinetta Newtonin laeille? Olkoon potentiaalienergia kuten alla kuvassa 1, eli potentiaalienergia on nolla ottamatta lukuun pientä
 :n korkuista mäennyppylää.
:n korkuista mäennyppylää.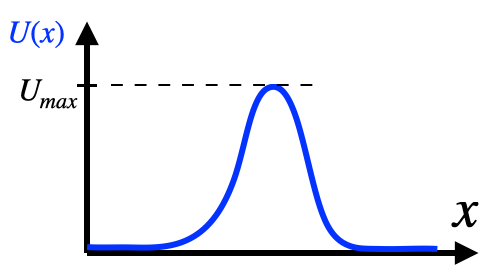
Kuva 1. Potentiaalivalli, jonka korkeus on
 .
.Olkoon lisäksi hiukkanen, jonka kokonaisenergia
 on pienempi kuin
on pienempi kuin  ja joka lähestyy potentiaalivallia vasemmalta. Kun tilannetta lähestytään klassisesti, hiukkasen on mahdotonta päästä potentiaalivallin ylitse. Kuvan 2 piste
ja joka lähestyy potentiaalivallia vasemmalta. Kun tilannetta lähestytään klassisesti, hiukkasen on mahdotonta päästä potentiaalivallin ylitse. Kuvan 2 piste  on
niin kutsuttu klassinen käännepiste, jossa potentiaalienergia on yhtä suuri kuin kokonaisenergia ja kineettinen energia on nolla; tässä pisteessä hiukkasen liikesuunta muuttuu ja se palaa tulosuuntaansa.
on
niin kutsuttu klassinen käännepiste, jossa potentiaalienergia on yhtä suuri kuin kokonaisenergia ja kineettinen energia on nolla; tässä pisteessä hiukkasen liikesuunta muuttuu ja se palaa tulosuuntaansa. 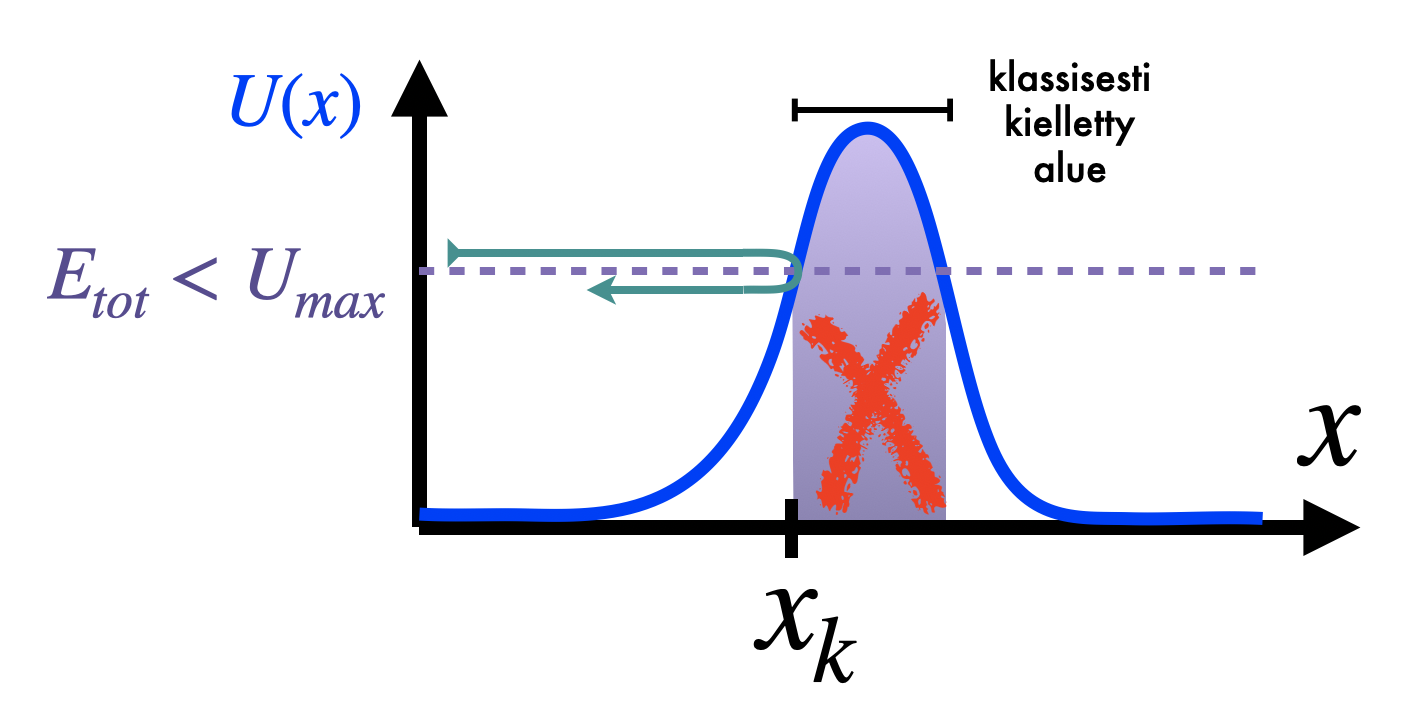
Kuva 2. Klassisen hiukkasen kääntyminen klassisessa käännepistessä
 , kun hiukkasen kokonaisenergia (katkoviivoilla esitetty
, kun hiukkasen kokonaisenergia (katkoviivoilla esitetty  ) on pienempi kuin potentiaalivallin korkeus (
) on pienempi kuin potentiaalivallin korkeus ( ). Varjostettu alue on klassisesti kielletty alue, jonne meneminen ei ole sallittua (kokonaisenergian säilyminen edellyttäisi negatiivista liike-energiaa).
). Varjostettu alue on klassisesti kielletty alue, jonne meneminen ei ole sallittua (kokonaisenergian säilyminen edellyttäisi negatiivista liike-energiaa).Eli kuten normaalisti tapahtuu ylämäkeen vieritetylle pallolle.
Aivan niin. Mutta kun tilannetta tarkastellaan kvanttimekaanisesti, hiukkanen voi kuin voikin päästä nyppylän ohi. Alla olevassa kuvassa on esimerkki hiukkasen aaltofunktiosta tällaisessa tilanteessa. Hiukkasen tulosuunnassa vasemmalla aaltofunktiolla on suuri amplitudi, joka pienenee klassisesti kielletyllä alueella, mutta säilyy nollasta poikkeavana myös nyppylän oikealla puolella: hiukkasella on todennäköisyystiheyttä myös nyppylän oikealla puolella. Siten hiukkanen on mahdollista havaita myös potentiaalivallin toisella puolella, vaikka vallin korkeus onkin hiukkasen liike-energiaa suurempi. Jos havaitaan mitataan vallin oikealla puolella, sanotaan, että hiukkanen on tunneloitunut potentiaalivallin läpi.
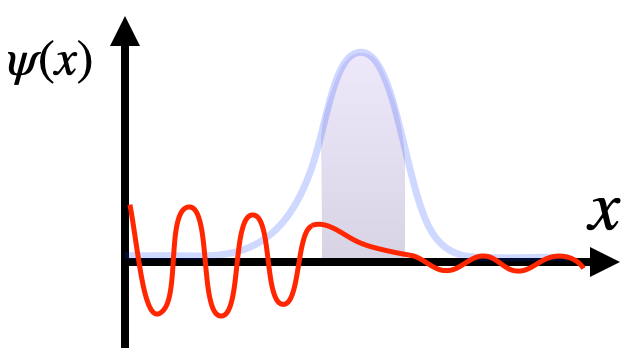
Kuva 3. Hiukkasen aaltofunktio tilanteessa, jossa potentiaalivalli on korkeampi kuin hiukkasen liike-energia. Todennäköisyysamplitudi poikkeaa nollasta vallin molemmin puolin.
Yllä oleva keskustelu ei välttämättä hätkäytä, mutta pohdi, mitä ilmiö tarkoittaisi klassisessa analogiassa: pyöräilet pienellä 10 km/h nopeudella kohti 100 m korkeaa mäkeä ja yllättäen huomaisit olevasi mäen toisella puolella — vaikka et polkenut edes lisävauhtia!
Video 1. Pyöräilijän tunneloituminen mäen läpi, mikä on klassisesti mahdotonta.
Joo, nyt kyllä ilmiön mystisyys alkaa valjeta.
Klassisesti tällainen tunneloituminen on toki mahdotonta. Kyseessä onkin puhtaasti kvanttimekaaninen ja käytännössä vain mikroskooppisissa tilanteissa aaltohiukkasille havaittava ilmiö. Juuri oppimamme aaltofunktion todennäköisyystulkintojen pohjalta tunneloituminen on kuitenkin jopa uskottavaa.
Nimittäin, esimerkiksi alla olevan kuvan rajaamassa alueessa hiukkanen löytyy (karkeasti arvioiden!) potentiaalivallin vasemmalta puolen 80% todennäköisyydellä, oikealta puolen 10 % todennäköisyydellä ja keskeltä potentiaalivallia, klassisesti kielletyltä alueelta 10% todennäköisyydellä. Hiukkastiheys on siis sijoittunut klassisesti kielletylle alueelle vain osittain, 10% todennäköisyydellä, joten ei haittaa vaikka hiukkasen kokonaisenergia olisikin pienempi kuin potentiaalivallin korkeus. Hiukkanen kun ei missään vaiheessa ole kielletyllä alueella kokonaan!
Kuva 4. Hiukkanen on klassisesti kielletyllä alueella vain osittain.
Klassisessa mekaniikassa tunneloitumista ei voi tapahtua, koska pistemäinen hiukkanen on omassa sijainnissaan aina kokonaan, 100 % todennäköisyydellä. Siksi pyöräilijäkään ei voi tunneloitua mäen läpi.
Ehkä paras klassinen analogia tunneloitumisella voisi olla seiväshyppy. Seiväshyppääjän painopiste ei nimittäin välttämättä missään vaiheessa käy riman yläpuolella. Silti seiväshyppääjä voi onnistua riman ylittämisessä — koska hyppääjä ei ole pistemäinen kappale!
Mutta tuo aaltofunktiohan tuossa vain jököttää paikallaan. Miten tunneloituminen oikein tapahtuu, miten hiukkanen etenee?
Staattiset kuvat eivät tosiaan ole omiaan havainnoimaan tunneloitumista. Kyseessähän on kuitenkin ajasta riippuva ilmiö, jossa hiukkanen liikkuu kohti seinää ja sitten siroaa siitä. Ilmiötä onkin paras tarkastella ajan funktiona, tehdään näin Videossa 2.
Video 2. Hiukkasen tunneloituminen potentiaalivallin läpi.
Entä se seinän läpäisy?
Mikä on "seinä"? Seinähän ei ole mitään muuta kuin potentiaalivalli: seinän molemmin puolin hiukkasen on helppoa olla eli potentiaalienergia on nolla, mutta seinän sisässä hiukkanen ei mielellään ole, eli potentiaalienergia on suuri.
Tunneloitumisen todennäköisyys kuitenkin pienenee eksponentiaalisesti potentiaalivallin korkeuden ja leveyden mukaan. Siksi riittävän paksujen esteiden läpäisy menee hyvin pian käytännössä hyvin epätodennäköiseksi.
Tunneloituminen ei ole täysin vähäpätöinen ilmiö, sillä siihen perustuu esimerkiksi auringon toiminta. Auringossa positiivisesti varatut ytimet hylkivät toisiaan Coulombin repulsion vuoksi, mikä aiheuttaa korkean potentiaalienergiavallin ytimien lähestyessä toisiaan. Useimmiten ytimien suhteellinen liike-energia ei riitä vallin ylittämiseen, jolloin ytimet kimpoavat takaisin erilleen. Joskus ytimet kuitenkin pääsevät läpäisemään vallin tunneloitumalla, jolloin ne pääsevät yhtymään eli fuusioitumaan. Tunneloitumistodennäköisyys on pieni mutta riittävä auringon toimintaan.
Lisäksi tunneloitumiseen perustuvat radioaktiiviset aineet, protonitunnelointi DNA:n mutaatioissa, tunnelidiodit ja -transistorit, tunneloitumismikroskoopit, ja niin edespäin. Katsotaan Videolla 3 lopuksi, miten tunneloituminen näkyy radioaktiivisen
 Pb-ytimen
alfahajoamisessa.
Pb-ytimen
alfahajoamisessa.
Video 3. Tunneloituminen mahdollistaa radioaktiivisen ytimen alfahajoamisen.
Yhteenveto:
- Kvanttimekaanisessa tunneloitumisessa hiukkanen voi läpäistä esteitä tavalla, joka on klassisesti mahdotonta.
- Tunnelointi on mahdollista, koska hiukkanen ei sijaitse klassisesti kielletyllä alueella kokonaan.
- Tunneloinnissa hiukkasen aaltofunktio poikkeaa nollasta potentiaalivallin molemmilla puolilla.
- Tunnelointi on käytännössä mahdotonta, kun este on liian korkea tai pitkä.
- Auringon energiantuotanto ja monet teknologiset sovellukset perustuvat tunneloimiseen.


