Edellisissä kysymyksissä (kysymys Onko kaikkialla maailmankaikkeudessa sama nykyhetki? ja Voiko avaruusmatkustaja vanheta maassa olevaa henkilöä hitaammin?) käsittelimme aikaa. Opimme, että aika on suhteellista, ja se kulkee eri tahdilla riippuen liikkeen suhteellisesta nopeudesta. Mitä suurempi suhteellinen nopeus liikkeellä on, sitä hitaammin liikkujan aika kulkee suhteessa paikalla olijaan.

Keskiössä on ollut ajan mittaaminen ja nopeuden vaikutus ajan kulkuun. Nopeushan määritellään tiettyyn matkaan kuluvana aikana, eli $v = s/t$. Jos nopeuden kasvaessa aika hidastuu liikkeen inertiaalikoordinaatiossa, auki on vielä se, miten nopeus vaikuttaa kuljettuun matkaan. Onko kahden pisteen välinen etäisyys kaikissa koordinaatistoissa sama?

Olet varmasti joskus mitannut erilaisia pituuksia, kuten esimerkiksi kaapin korkeuden, oven leveyden tai vaikka tikkaiden pituuden. Niiden mittaaminen on aika helppoa. Millä tavalla ajan suhteellisuus vaikuttaa sitten esimerkiksi tikkaiden pituuteen? Isa ja Uno yrittävät nyt ajan suhteellisuuden innoittamina tutkia, onko mahdollista saada $10$ m pituiset tikapuut vaakatasossa $9$ m pitkään varastoon. Mitähän tässä tapahtuu?

Mitä arvelet: Millä keinolla tikkaat mahtuisivat varastoon? Vai onko tämä mahdotonta?

Seurataanpa Isan ja Unon välistä keskustelua aiheesta:

Uno: "Tuossa ei ole kyllä mitään järkeä, että $10$ m pitkät tikkaat mahtuisivat $9$ m pitkään varastoon..."

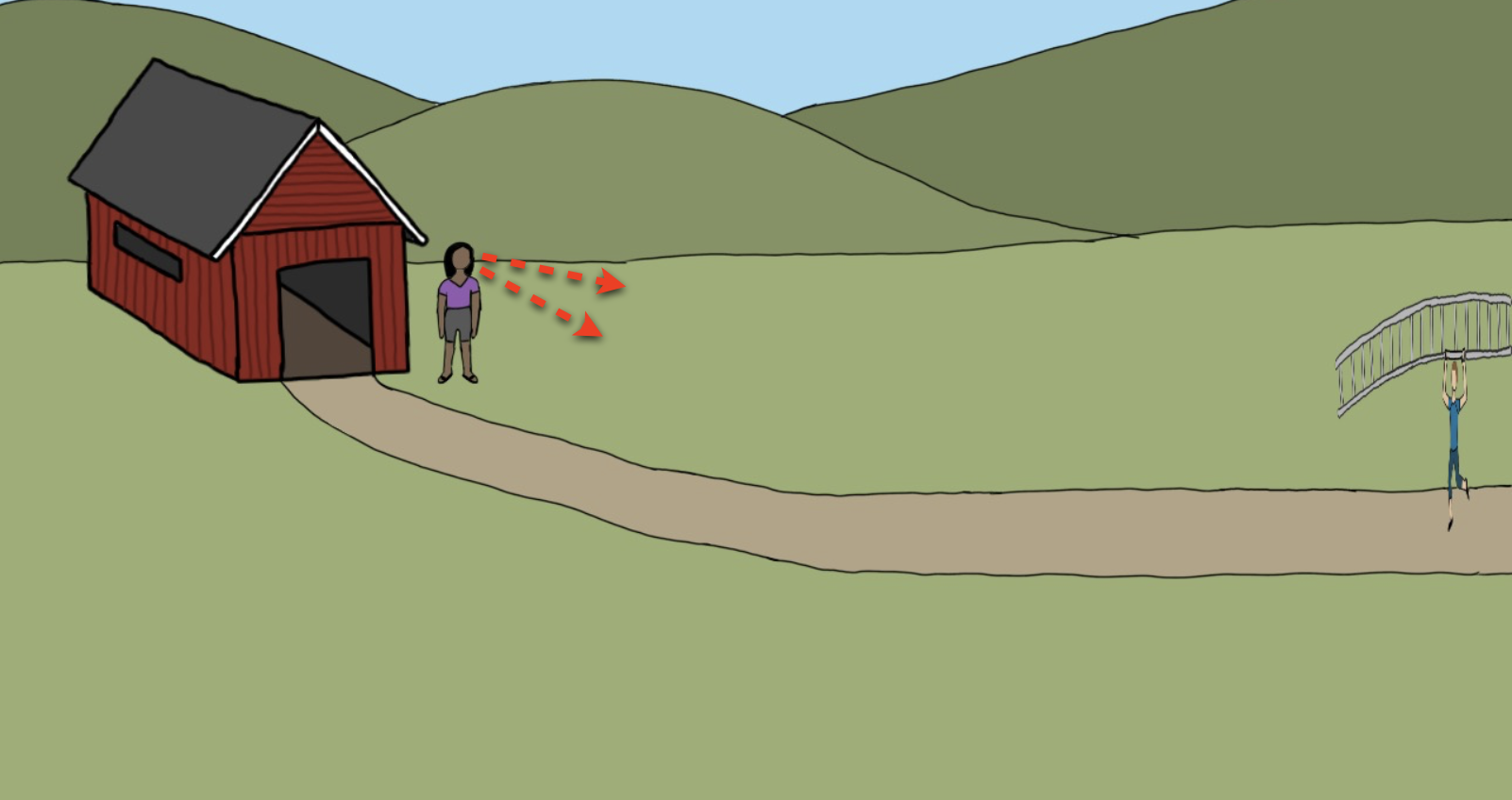
Kuva 1. Isa seisoo varaston nurkalla, Uno seisoo tikapuut käsissään.

Isa: "Ei olekaan. Mutta aiemmissa tehtävissähän puhuttiin ajasta ja nopeuksista. Mitenköhän asioiden nopeudet vaikuttavat tässä?"

Uno: "Tarkoitatko tikkaiden ja varaston nopeuksia?"

Isa: "Niin. Jos on $10$ m pitkät tikkaat, joita yritetään laittaa vaakatasossa $9$ m pitkään varastoon, niin eihän se tietenkään onnistu. Mutta mitä jos juokset tikkaiden kanssa varastoon todella nopeasti?"

Uno: "Miten se voisi vaikuttaa asiaan?"

Isa: "Kaksosparadoksissahan (Voiko avaruusmatkustaja vanheta maassa olevaa henkilöä hitaammin?) suurella nopeudella kulkijan aika hidastuu ulkopuolelta katsottuna. Ajan kulku riippuu tarkastelijan näkökulmasta. Näyttävätkö tikkaat erilaiselta meidän näkökulmistamme, jos minä seison varaston vieressä ja sinä juokset niiden kanssa? Mitä kumpikin meistä näkee?"

Uno: "Tietenkin näet, että minä tikkaineni liikun sinua ja varastoa kohti!"

Isa: "Niin tietenkin, mutta mietitäänpä samaa tilannetta toisesta näkövinkkelistä: Jos sinä juokset kohti varastoa tikkaiden kanssa ja minä seison varaston vieressä, niin miltäköhän tilanne sinun eli juoksijan näkökulmasta näyttää?"

Uno: " Näen tietenkin varaston ja sinun lähestyvän itseäni, jos itse kuvittelen olevani levossa."

Isa: "Niinpä, käy edelleen järkeen. Entä mitä tikkaille tapahtuu?"

Uno: "Ei kai tikkaille pitäisi tapahtua mitään, tikkaat vain kulkevat mukanani."

Isa: "Periaatteessa näin, eli tikkaisiin ei voi yhtäkkiä esimerkiksi tulla lisää tai hävitä ainetta."

Uno: "No, niinpä. Tikkaat siis eivät mahdu varastoon?"

Isa: "Tältähän se tuntuisi. Mutta entäpä suhteellisuusteoreettiset ilmiöt?"

Uno: "Mitä ihmettä? Eihän tämä tilanne liity mihinkään avaruuteen!"

Isa: "Ei liitykään. Mutta miksi suhteellisuusteoreettisten ilmiöiden pitäisi liittyä vain avaruuteen? Tehdäänpä uusi ajatuskoe: Sinä juokset siis minua ja varastoa kohti tikkaat vaakatasossa käsissäsi. Tikkaiden pituus mitattuna niiden levätessä maassa on $10$ m. Mahtaisiko tikkaiden pituus muuttua omasta näkökulmastasi?"

Isa: "Omasta mielestäsi tikkaiden pituutena pysyy $10$ m; ne ovat edelleen sinun suhteesi levossa. Jatketaanpa kuvittelua: Ajatellaan, että minä pystyisin myös jotenkin mittaamaan tikkaiden pituuden samalla kun sinä juokset niiden kanssa. Mitä luulet, minkähän pituuden saisin tikkaille mitattua?"

Uno: "Tikkaat siis näkökulmastasi lyhenisivät?! Vaikuttaisi ilmeiseltä, että mittaisit tikkaiden pituudeksi niiden alkuperäisen pituuden eli $10$ m. Miksei näin käykään?"

Isa: "Tikkaat lyhenevät suhteellisuusteoreettisista syistä, tarkemmin sanottuna kyse on ilmiöstä nimeltä pituuskontraktio. Se tarkoittaa sitä, että kappaleen pituus riippuu havainnoijan liiketilasta suhteessa kappaleeseen. Kappaleen suhteen liikkeessä oleva havaitsija mittaa kappaleen pituuden lyhyemmäksi kuin kappaleen suhteen levossa oleva havaitsija.

Uno: "Pituuskontraktio, olen joskus kuullut sen sanan. Termi "kontraktio" taitaa viitata kasaanmenemiseen, supistumiseen tai lyhenemiseen. Tämän pituuskontraktion suuruuden voi varmaan jotenkin laskea?"

Isa: "Kyllä vaan. Katsotaanpa pituuskontraktion tarkastelemisesta pieni videonpätkä. "

Video 1. Pituuskontraktion johtaminen aikadilaation lausekkeen avulla.

Toistetaan pituuskontraktion yhtälö vielä kertaalleen:

$l=l_0/\gamma=l_0\sqrt{1-v^2/c^2}$.

Tämä yhtälö kuvaa kappaleen pituuden ja nopeuden riippuvuutta toisistaan liikkeen ulkopuolisen tarkkailijan koordinaatistossa. Sen avulla voidaan laskea minun eli ulkopuolisen havaitsijan havaitsema tikkaiden pituus $l$, kun sinä Uno tikkainesi liikutte tietyllä nopeudella $v$. Pituus $l_0$ on kappaleen (tai etäisyyden) lepopituus: se on kahden pisteen välinen etäisyys, pisteiden suhteen levossa mitattuna. $\gamma$ on aiemmista kysymyksistä tuttu suhteellisuusteoreettinen tekijä. Meidän tapauksessamme nämä pisteet ovat tikkaiden etupää ja takapää. Koska juokset tikkaiden kanssa, niiden päät ovat sinun koordinaatistossasi levossa ja havaitset tikkaiden lepopituudeksi $l_0 = 10$ m. Mitä lähempänä tikkaiden nopeus on valonnopeutta $c$, sitä lyhemmäksi tikkaat ulkopuolisen havaitsijan näkökulmasta kutistuvat. Liikettä katseleva ja paikoillaan oleva havaitsija näkee siis liikkuvan kappaleen litistyvän eli kontraktoituvan liikkeen suunnassa."

Uno: "Ulkopuolisen havaitsijan eli sinun silmin tikkaiden pituus siis oikeasti lyhenee."

Kuva 2. Kun Uno juoksee lujaa Isaa kohden, Isa näkee kontraktoituneena sekä tikapuut että Unon.

Isa: "Kyllä, ihan oikeasti. Ja toisaalta jos asiaa tarkastellaan sinun näkökulmastasi niin mielestäsi varasto taas lyhenee, sillä se liikkuu suhteessa sinun koordinaatistoosi! Tai itse asiassa mielestäsi koko ympäristö lyhenee, koska liikut suhteessa kaikkeen muuhunkin."

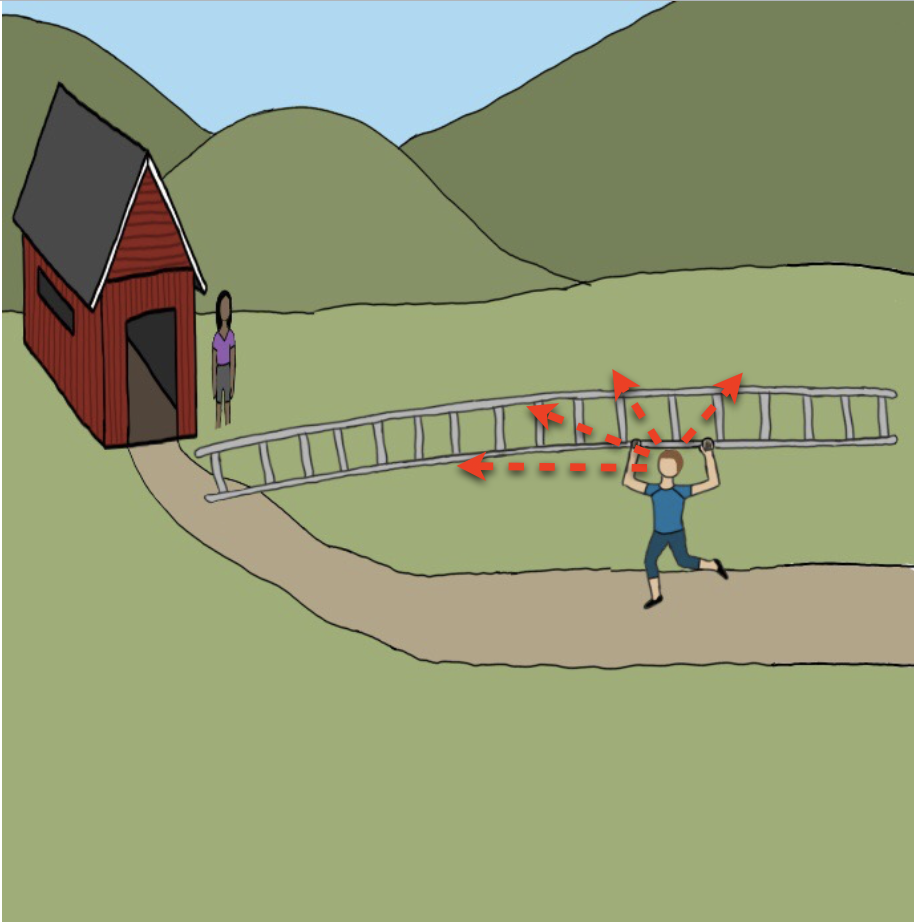
Kuva 3. Isaa kohden lujaa juokseva Uno näkee Isan, varaston ja koko ympäristön  juoksusuuntaan kontraktoituneena.

Uno: "Voimme siis laskea pituuskontraktion yhtälön avulla, millä nopeudella varastoon olisi juostava, jotta tikkaiden pituus sinun näkökulmastasi olisi $9$ m?"

Isa: "Näin on, eli lasketaanpa."

Uno: "Yhtälöstä ratkaistaan nyt siis $v$... Saadaan $v = c\sqrt{1-l^2/l_0^2}$ ja sijoitetaan $l = 9$ m ja $l_0 = 10$ m ja tällöin nopeudeksi saadaan $0{,}436c$. "

Isa: "Se tarkoittaa, että juoksunopeuden olisi oltava lähes 44 % valonnopeudesta."

Uno: "Sehän on mahdottoman suuri nopeus!"

Isa: "Joo, eikä toki lainkaan realistinen. Mutta jos keino olisi, niin tällä nopeudella tikkaat olisivat näkökulmastani yhdeksän metriä pitkiä. Silloin ne mahtuisivat varastoon. Mietitäänpä tilannetta vielä vähän tarkemmin jos se auttaisi sinua ymmärtämään asiaa. Mitä ensinnäkin tarkoittaa se, että tikkaat mahtuvat varastoon?

Uno: "No varmaan sitä, että jos varaston ovet laitettaisiin kiinni, niin tikkaat olisivat ovien välissä eli varaston sisäpuolella.

Isa: "Joo, olen samaa mieltä. Ja jos mietitään tilannetta, jossa tikkaat mahtuvat juuri ja juuri varastoon, niin silloin ulkopuolisen tarkkailijan mielestä tikkaiden takapää menee ovien sisäpuolelle samalla hetkellä kuin tikkaiden etupää tulee varastosta ulos. Mutta jos sinä juokset itse tikkaiden kanssa, niin sillä hetkellä kun havaitset tikkaiden etupään tulevan varastosta ulos, sinusta näyttää, että tikkaiden takapää on vielä kaukana varaston ulkopuolella. Mikä tämän selittäisi?

Uno: "Minäpä arvaan tuon! Tämä liittyy varmaan siihen, että emme voi päätellä, että yhdessä koordinaatistossa samanaikaiset tapahtumat olisivat samanaikaisia muissa koordinaatistoissa. (katso kysymys Onko kaikkialla maailmankaikkeudessa sama nykyhetki?).

Isa: "Olet aivan oikeassa! Nämä kaksi tapahtumaa, eli tapahtuma 1 = tikkaiden etupää varaston takaseinän kohdalla ja tapahtuma 2 = tikkaiden takapää varaston oven suun kohdalla eivät ole eri koordinaatistoissamme samanaikaisia. Tällöin sinä oikeasti koet, etteivät tikkaat mahdu varastoon ja minä oikeasti koen, että tikkaat mahtuvat. Tarkkaan ottaen havaitsemisessa pitäisi huomioida vielä lisäksi aika, joka valolla kuluu kulkea tikkaiden etu- ja takapäästä silmiisi.

Uno: "Uskomatonta! Mutta onko tämä totta? Vai onko kyseessä vain jokin ovela visuaalinen harha? Minä itsehän kuitenkin näen juostessani tikkaat edelleen $10$ m mittaisina."

Isa: "Niin, totta. Minä katselijana katson tilannetta omasta näkökulmastani ja sinä Uno juoksijana omastasi. Tikkaat ovat omasta mielestäsi edelleen $10$ m:n mittaiset, ja varasto on jopa aiempaa lyhyempi. Onko jompikumpi näkökulma oikeampi?"

Uno: "Se on varmaan se korrekti näkökulma tai koordinaatisto, jossa kukaan tai mikään ei liiku."

Isa: "Mutta entä jos mietittäisiin tilannetta jossa kukaan ei liiku. Minkä suhteen ne eivät siis liiku?"

Uno: "Toistensa suhteen. Jos kumpikaan henkilöistä ei liiku ja varastokaan ei liiku."

Isa: "Mutta silloinhan kaikki ovat liikkumatta vain, kun katsotaan Maan näkökulmaa. Entä, jos katsotaan tilannetta Auringosta käsin?"

Uno: "Auringosta käsin näkee Maan liikkuvan ja siten myös henkilöiden ja varaston liikkuvan..."

Isa: "Niinpä. Aina on jokin muu, jonka näkökulmasta liikettä on."

Uno: "Miten tämän paradoksisen tilanteen siis voi ymmärtää?"

Isa: "Emme voi sanoa jonkin olevan täysin paikoillaan kaiken suhteen. Absoluuttista lepokoordinaatistoa, eli kaiken suhteen levossa olevaa koordinaatistoa, ei voi määritellä. Siispä ei voida sanoa, että yhden näkökulma on oikeampi kuin toisen"

Uno: "Eli emme voi sanoa, ovatko tikkaat $9$ m vai $10$ m mittaiset?"

Isa: "Kyllä voimme — meidän vain tulee hyväksyä, että pituus riippuu siitä kuka sitä mittaa! Pituus voi siis olla yhtä aikaa $9$ m ja $10$ m. Ulkopuolinen katselija näkee tikkaat $9$ m mittaisina ja tikkaiden kanssa juoksija $10$ m mittaisina. Nämä havainnot tapahtuvat samanaikaisesti eivätkä ole ristiriidassa keskenään, aivan kuten aikadilaation yhteydessä ajankulku oli suhteellista ja riippui liikkeen nopeudesta."

Uno: "Hämmentävää! Ulkopuolisen silmin tikkaat siis mahtuvat varastoon, mutta tikkaiden kanssa juoksijan mielestä eivät! Ja kontraktiohan tosiaan toimii myös toisin päin, kun juoksija näkee varaston lyhenevän. Juoksijan näkökulmasta varasto lähestyy häntä nopeudella $0{,}436c$, jolloin pituuskontraktio tapahtuu myös varastolle, samoin kuin koko ympäristölle. Mutta mistä tämä koko ilmiö johtuu? Miksi nopeus vaikuttaa tällä tavalla pituuteen? "

Isa: "Pituuskontraktio on ikään kuin aikadilaation sisarilmiö. Kysymyksessä Voiko avaruusmatkustaja vanheta maassa olevaa henkilöä hitaammin? käsiteltiin myonien liikettä ilmakehässä. Myonien odotettua suurempi määrä merenpinnan tasolla selitettiin aikadilaation avulla siten, että koska ne liikkuivat lähes valonnopeudella, aikadilaation vuoksi niiden koordinaatistossa aikaa kuluikin vähemmän kuin tutkijat odottivat ja odotettua harvempi myoni ehti hajoamaan. Samaa tilannetta voidaan tulkita myös pituuskontraktion kannalta: koska myonit liikkuvat lähes valonnopeudella, myonien lepokoordinaatistossa matka vuoren huipulla sijainneesta mittalaitteesta merenpinnalla sijaitsevalle mittalaitteelle lyhyempi kuin Maan koordinaatistossa. Asetelmaa voi verrata havaitsemaasi varaston ja ympäristön lyhenemiseen juostessasi varastoa kohden myonin tavoin valtavan lujaa. Tällöin myonien suuri määrä merenpinnalla voidaan selittää aikadilaation lisäksi myös pituuskontraktion avulla.

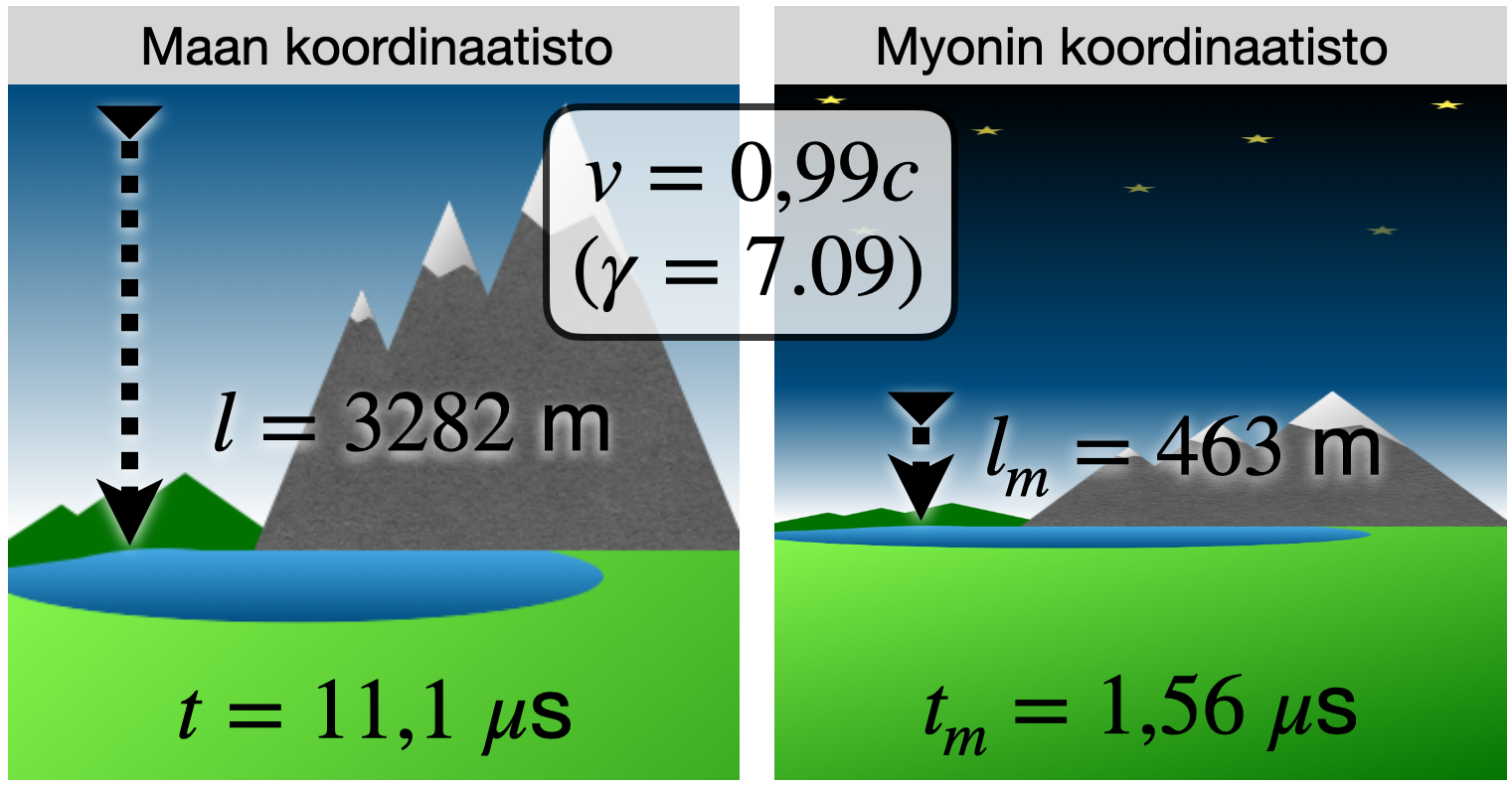
Kuva 4. Myonien aikadilaatio. Myonit kulkevat nopeudella 0,99c ($\gamma=7,09$) ylhäältä alas, joten ne liikkuvat Maan koordinaatistossa 3282 m:n korkuisen vuoren ohitse 11,1 $\mu$s:ssa. Myonien puoliintumisaika on 1,56 $\mu$s, joten voisi kuvitella, että vuoren juurella mitattu myonien määrä on murto-osa ($(1/2)^{11,1/1,56}$~1%) vuoren laella mitatusta myonien määrästä. Hiukkasen puoliintumisaika (~elinaika) kuitenkin liittyy ajan mittaukseen hiukkasen lepokoordinaatistossa! Maan lepokoordinaatistossa 3282 m:n korkuinen vuori on myonien lepokoordinaatistossa kontraktoitunut ja vain 463 m:n korkuinen. Siten vuoren ohittamiseen myonien lepokoordinaatistossa kuluu vain 1,56 $\mu$s. Siksi myonien määrä vuoren laelta sen juurelle mentäessa ainoastaan puolittuu.

Matkan lyheneminen suurilla nopeuksilla on siis verrattavissa ajan hidastumiseen. Molempien ilmiöiden kautta saamme näkökulman myös siihen, miksi valonnopeutta ei voi saavuttaa. Kun nopeus lähestyy valonnopeutta $v\rightarrow c$, matka lähestyy nollaa $s \rightarrow 0$ samalla kun aika lähestyy ääretöntä $t \rightarrow \infty$. Valonnopeutta ei voi saavuttaa, sillä pituus ei voi kutistua täysin olemattomiin, eikä aika voi hidastua täysin pysähdyksiin."

Uno: "Onpa mielenkiintoista! Kiitos keskustelusta."

Toivottavasti Unon ja Isan keskustelu osoitti, miten ajan lisäksi myös etäisyys on suhteellista ja riippuu liikkeen nopeudesta.

Yhteenveto:

• Pituuskontraktiolla tarkoitetaan ilmiötä, jossa liikkuva kappale lyhenee liikkeen suuntaisesti ulkopuolisen havaitsijan koordinaatistosta tarkasteltuna.
• Pituuskontraktion yhtälö on $l = l_0/\gamma=l_0 \sqrt{1-v^2/c^2}$, missä  $v$ on liikkeen nopeus, $l_0$ on kappaleen ominaispituus ja $l$ on kappaleen pituus ulkopuolisen havaitsijan koordinaatistosta tarkasteltuna.
• Pituuskontraktion vaikutuksesta myös liikkeen inertiaalikoordinaatiosta tarkasteltuna kahden pisteen välinen välimatka lyhenee nopeuden kasvaessa.
• Absoluuttisesti levossa olevaa koordinaatistoa ei voi määrittää.
• Pituuskontraktion vaikutukset ovat merkittäviä vasta nopeuden lähestyessä valonnopeutta.
• Kappaleen pituutta mitatessa tulee hyväksyä, että pituus riippuu mittaajan liiketilasta.