Viime viikolla kotiin kävellessä minut yllätti rankkasade. Aloin automaattisesti juosta, mutta aloin jälkikäteen pohtia, että onko juokseminen sittenkään kannattavaa. Onko kastumisen kannalta väliä käveleekö vai juokseeko?

Alkukantaiset vaistot tosiaan saavat helposti tilanteessa juoksemaan, mutta on hyvä pohtia miettimään mikäli se kannattaa aina.

Tarkastellaan ensin suoraan alaspäin satavaa sadetta. Alas satavat sadepisarat eivät ensinnäkään ole pisaran muotoisia, vaan jokseenkin pyöreitä (Kuva 1). Ajatus pisaran muodosta taitaa juontaa juurensa siitä miltä pisarat näyttävät hanasta tai lehtien puilta juuri ennen irtoamistaan. Pisarat tulevat alaspäin vakionopeudella, pisaroiden terminaalinopeudella. Terminaalinopeuden saavuttaminen vastaa tilannetta, jossa pisaraan kohdistuvat Maan vetovoima ja ilmanvastusvoima ovat yhtä suuria ja vastakkaissuuntaisia; tällöin pisara ei kiihdy, vaan nopeus säilyy vakiona. (Pisarat saavuttavat terminaalinopeuden yleensä jo muutaman muutaman metrin matkalla.) Terminaalinopeuden suuruus riippuu pisaroiden koosta. Tyypillisessä kesäsateessa pisaroiden nopeus on parikymmentä kilometriä tunnissa ($v_y\sim -5\; m/s$) ja pisaroiden halkaisija on muutama millimetri. Pisaroiden koko ja nopeus riippuvat voimakkaasti sateen luonteesta.

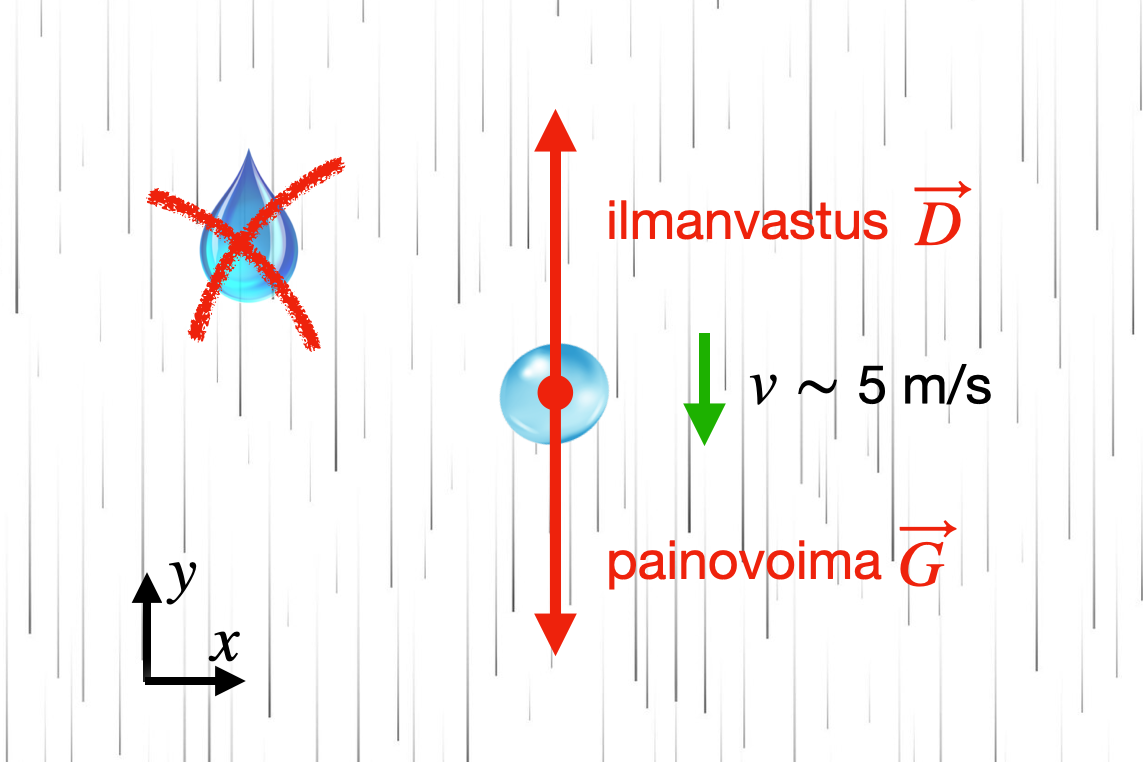
Kuva 1. Alas satava pisara on pyöreä, ei pisaranmuotoinen. Pisara etenee alaspäin tasaista nopeutta, jolloin painovoima alaspäin ja ilmanvastusvoima ylöspäin ovat yhtä suuret. Pisaran nopeus on tyypillisesti joitakin metrejä sekunnissa, mutta se riippuu pisaran koosta.

Paljonko pisaroita rankkasateessa muuten on?

Rankkasateeksi luokittelu riippuu sekä veden määrästä että sateen kestosta. Vesisateessa satavan veden määrää kuvataan millimetreinä aikayksikössä. Nämä millimetrit kuvaavat sen “vesipatjan” korkeutta, joka sateesta aiheutuisi jos yhtään sadevettä ei imeytyisi maahan. Erilaiset sademittarit mittaavat juuri tämän vesipatjan korkeutta.

Rankkasateita ovat esimerkiksi 

• $2,5$ minuutissa $5$ mm:n sade ($2$ mm/min), 
• tunnissa $7{,}0$ mm:n sade ($0{,}12$ mm/min) tai 
• vuorokaudessa $20$ mm:n sade ($0{,}014$ mm/min). 

Tarkastellaan tuota kovinta hetkellistä sadetta, $2$ mm/minuutti. Pisaroiden nopeudella $v_y=-5\; m/s$ ne putoavat maahan minuutin kuluessa laskennallisesti $300$ m:n korkeudelta. Vettä ilmassa tilavuuden suhteen on siten $\eta=2\; mm/300\;m=7\times 10^{-6}$ eli seitsemän miljoonasosaa, seitsemän millilitraa kuutiometrissä. Jos pisaran koko on $3$ mm, niin seitsemän millilitraa tarkoittaa $500$ pisaraa kuutiometrissä eli kahden litran ilmatilavuutta pisaraa kohden, siis pisaroita noin $\sim 13$ cm:n etäisyyksillä toisistaan.  Samoin heikommille rankkasateille

• $0{,}12$ mm/min sateelle tiheys $\eta=4\times 10^{-7}$ ($30$ pisaraa/m$^3$ eli $30\;l/$pisara, $\sim 30\; cm$ etäisyyksillä toisistaan)
• $0{,}014$ mm/min sateelle tiheys $\eta=5\times 10^{-8}$ ($3$ pisaraa/m$^3$ eli $300\;l/$pisara, $\sim 70\; cm$ etäisyyksillä toisistaan) 

jos pisaran koko oletetaan vakioksi (mikä saattaa olla huono arvio, sillä pisaran koko usein kasvaa sateen muuttuessa kovemmaksi).

No eipä ole tullut mietittyä sadetta tuolta kantilta. Pisarat ovat oikeasti aika harvassa, vaikka kaksi milliä minuutissa on todella rankkaa sadetta.

Sivuhuomautuksena voisi myös mainita, että normaalissa lämpötilassa ja ilmanpaineessa ilmamolekyylitkin vievät $\sim 25\times 10^{-6}$ osan tilavuudesta, eli yli kymmenen kertaa enemmän kuin vesipisarat $2{,}5$ minuutin rankkasateessa tai lähes tuhat kertaa enemmän kuin vesipisarat vuorokauden rankkasateessa. Sateen voi siis sanoa olevan todella harvaa.

Mutta silti se kyllä kastelee.

No niin tekee. Tuolla $2\; mm/min$ sateella neliömetrin kokoiseen vesilätäkköön osuisi $2500$ ja kämmenen pinnalle ($\sim 100\; cm^2$) $25$ pisaraa sekunnissa. Kyllä siinä märäksi tulee.

Mutta jatketaan tähän suuntaan ja tarkastellaan kastumista yleisesti. Jos seisomme suoraan alaspäin satavassa sateessa, kastumme vain päältämme. Kun pisaroiden nopeus on $v_y=-5\; m/s$, sateen vesitiheys $\eta\sim 1\times 10^{-6}$ ja kun päämme ja hartioidemme pinta-ala on $A_y\sim 1300\; cm^2$, niin päällemme satavan veden määrä on $\eta |v_y| A_y=0{,}7$ millilitraa sekunnissa. Voidaan puhua myös satavan veden vuosta pinnan $A_y$ läpi. Tämä vesimäärä sisältyy kuvan 2 varjostettuun tilavuuteen.

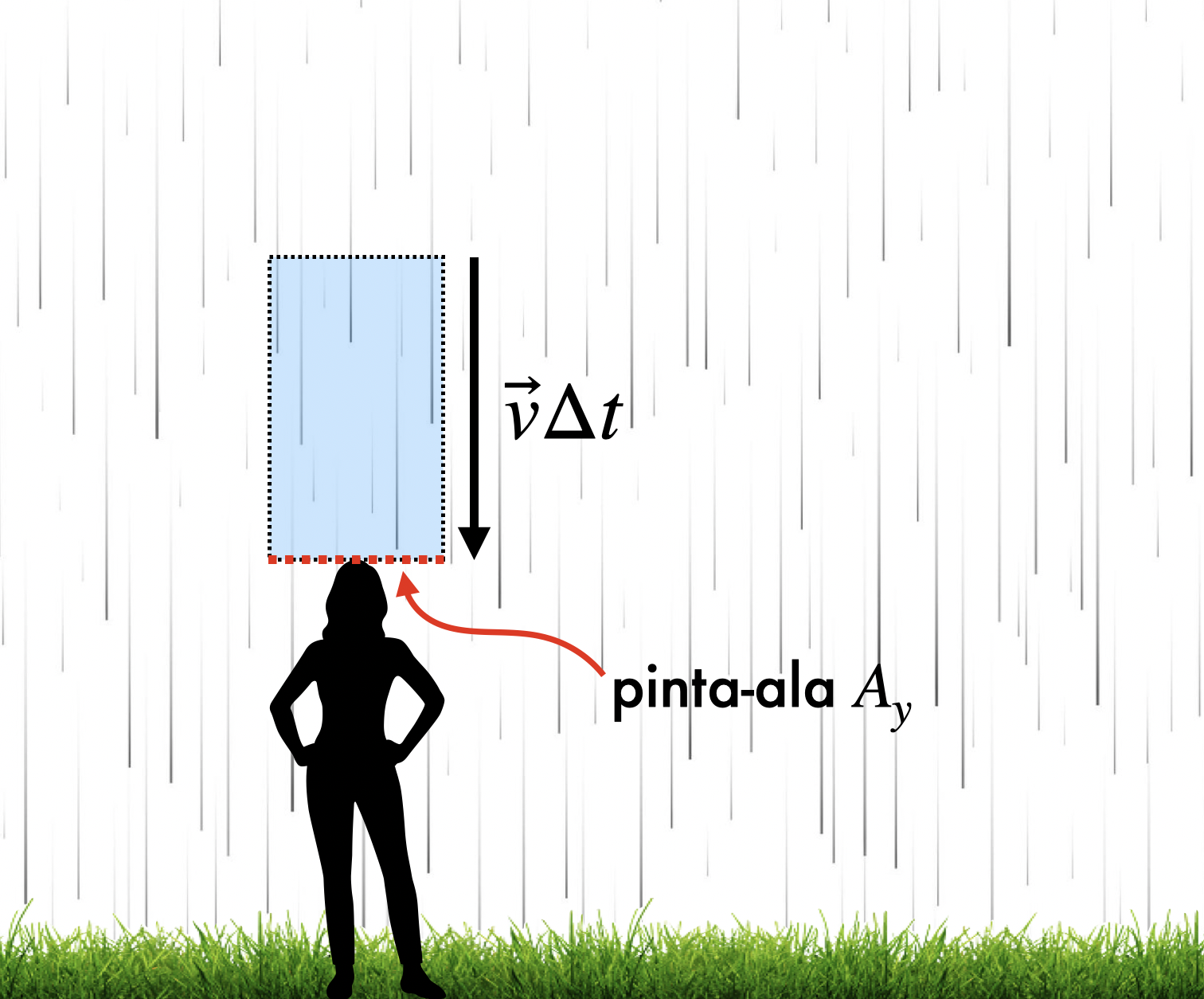
Kuva 2. Sataa suoraan alaspäin. Aikavälin $\Delta t$ aikana hartioille sataa varjostettuun tilavuuteen sisältyvät vesipisarat.

Entä se liikkuminen sateessa?

Hyvä, jatketaan siis eteenpäin. Tarkastellaan samaa, suoraan alaspäin tulevaa sadetta samalla kun kävelet reippaasti eteenpäin (oikealle) nopeudella $u_x=u=2\; m/s$. Tällöin kävelet kohti edessä olevia sadepisaroita, jolloin kastumme myös etuosastamme (Kuva 3).

Kuva 3. Kastuminen kävellessä, suoraan alaspäin tulevassa sateessa.

Hartioillemme tuleva vesimäärä on $\eta V_y = \eta |v_y|\Delta t A_y$, aivan kuten sateessa pelkästään seistessä. Etuosaamme tuleva vesimäärä on $\eta V_x=\eta |u| \Delta t A_x$, joka kasvaa nopeuden kasvaessa: mitä lujempaa juoksemme, sitä nopeammin kastumme.

Tästä voisimme jo tehdä arvion kokonaiskastumiselle suoraan alaspäin tulevassa sateessa, kun kuljettava matka on $L$. Matkaan kuluva aika $\Delta t=L/u$, joten kastuminen on yhteensä 

Hartiamme siis kastuvat sitä vähemmän mitä nopeammin juoksemme (ensimmäinen termi, $\propto 1/u$). Toisaalta etuosamme kastuu saman verran juoksunopeudesta riippumatta (toinen termi, $\eta L A_x$). Nopeasti juostessamme etuosa kastuu nopeammin (tekijä $u$ osoittajassa), mutta pääsemme myös nopeammin perille (tekijä $u$ nimittäjässä). Nämä vastakkaiset pyrkimykset kumoutuvat ja aiheuttavat kastumisen, joka on nopeudesta riippumaton.

Entä kun ei sada suoraan alaspäin, vaan tuulee?

Ok, lisätään malliimme uusia elementtejä. Mikäli tuuli on tasaista (eikä puuskaista), voimme olettaa sadepisaroiden etenevän tuulen kanssa samaa nopeutta. Tuulkoon esimerkissämme vasemmalle, jolloin sateella on negatiivinen vaakasuora komponentti, vaikkapa $v_x=-2\; m/s$. Pystysuoran komponentin $v_y=-5\; m/s$ voimme olettaa säilyvän jokseenkin ennallaan. Sataa siis vasemmalle viistoon $22$ asteen kulmassa suhteessa pystysuoraan. Fyysikot lähestyvät tällaisia tilanteita perinteisesti koordinaattimuunnosten avulla.  (Toisessa MOOC-kurssissamme Kvanttimekaniikkaa ja suhteellisuusteoriaa yleissivistävästi tarkastelemme mitä kummallista tapahtuu, kun koordinaatistot liikkuvat toistensa suhteen lähes valon nopeudella!) Kun sateen nopeusvektori on $\vec{v}$ ja henkilön kävelynopeusvektori $\vec{u}$, henkilö havaitsee sateen tulevan suunnassa $\vec{v’}=\vec{v}-\vec{u}$ omassa koordinaatistossaan (Kuva 4).

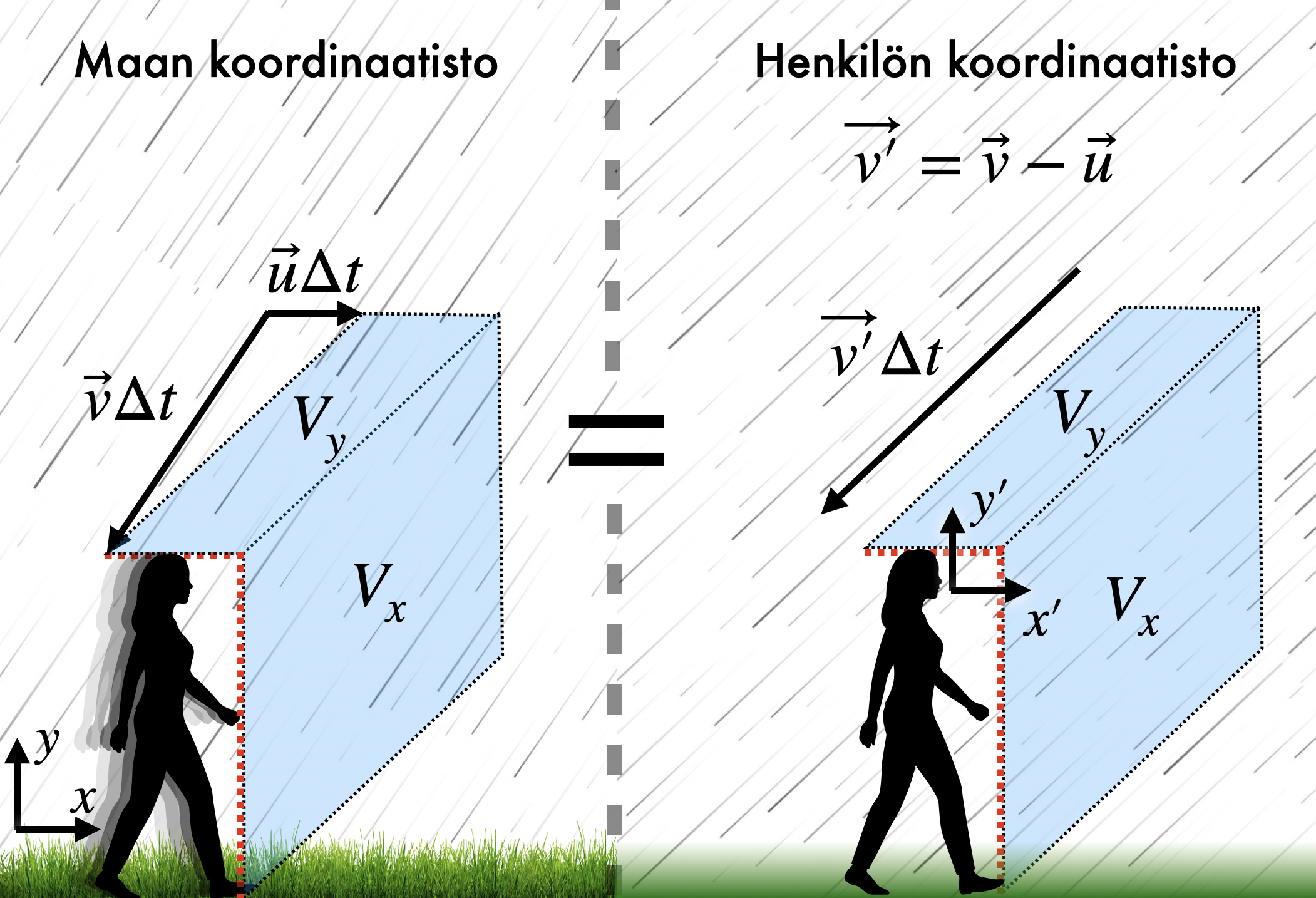
Kuva 4. Maan koordinaatistossa sateen nopeus on $\vec{v}$, samalla kun henkilö kävelee nopeudella $\vec{u}$. Tämä tilanne on kastumisen kannalta ekvivalentti tilanteen kanssa, jossa henkilö on paikallaan ja sateen nopeus on $\vec{v}'=\vec{v}-\vec{u}$.

Tilavuus $V_y$ on tässäkin tilanteessa sama kuin edellä, joten päällemme satavan veden määrä ei riipu sateen suunnasta (koska oletimme veden nopeuden pystysuora komponentin olevan tuulesta riippumaton). On ilmeistä, että etuosamme saama veden määrä $\eta V_x=\eta |v_x-u|A_x\Delta t$ kasvaisi ajan mukana vaikka olisimme paikallamme ($u_x=0$). Veden määrä etuosaan (tai takaosaan) kasvaa kun nopeuksien erotuksen itseisarvo ($|v_x-u|$) kasvaa.

Entä jos kävelemme myötätuuleen tuulen nopeudella? Tällöin erotus olisi nolla ja pääsisimme sadetta karkuun?

Kyllä. Kun kävelemme samaa nopeutta kuin sateen vaakasuora komponentti ($u=v_x$), etuosaamme (tai takaosaamme) ei osu vettä lainkaan (Kuva 5).

Kuva 5. Kun kävelemme myötätuuleen tuulen nopeutta hitaammin, takaosamme kastuu (vasen). Kun kävelemme sateen suuntaan täsmälleen samaa vauhtia kuin sateen vaakasuora komponentti, kastumme vain yläosastamme (oikea).

Yleisessä tapauksessa kastumisen määrä eli veden kokonaisvuo pintojen $A_x$ ja $A_y$ läpi $L$:n mittaisella matkalla ja tuulen nopeudella $v_x$ eli sateen nopeudella $v_x\hat{i}+v_y\hat{j}$ on 

Oletetaan veden määrä ilmassa $\eta=10^{-6}$, yläosan pinta-ala $A_y= 0{,}13\; m^2$, etu- ja takaosan pinta-ala $A_x=0{,}7\; m^2$, sateen nopeus $v_y=-5\; m/s$ ja kuljettava matka $L=100\;m$. Kuvaan 6 on piirrettynä muutama käyrä kastumisen määrästä erilaisilla vastaisilla ja myötäisillä tuulen nopeuksilla. Vastatuuleen kulkiessa kastumme sitä vähemmän mitä nopeampaa liikumme. 

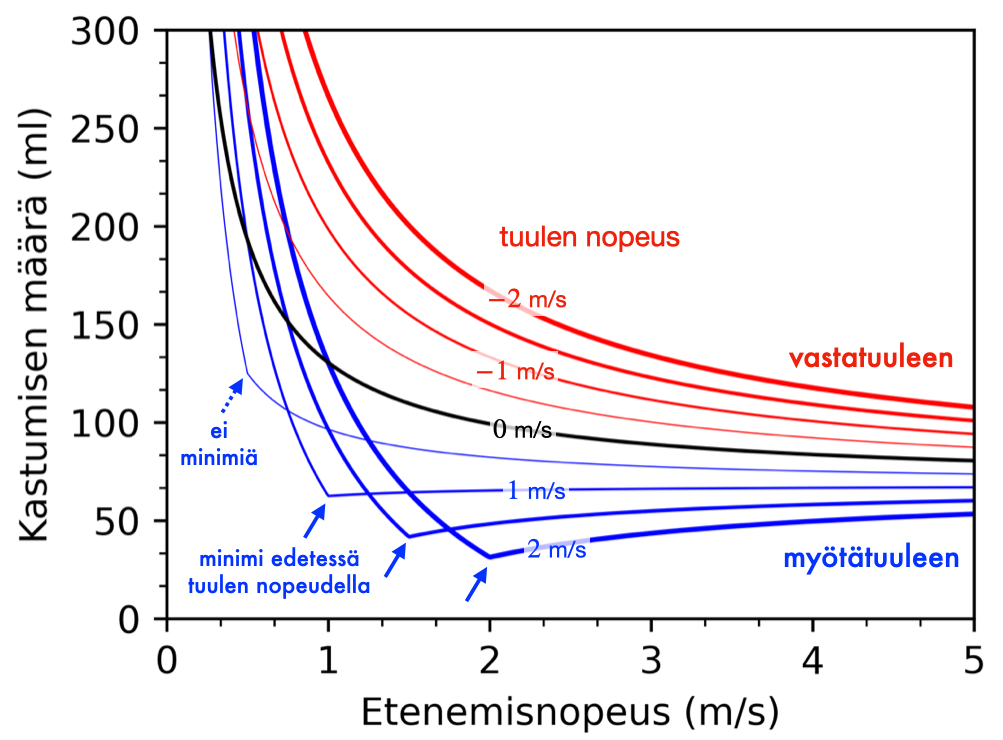
Kuva 6. Kastumisen määrä etenemisnopeuden funktiona tekstissä oletetuilla parametrien arvoilla ja erilaisilla tuulen nopeuksilla vastatuuleen (punaiset käyrät), myötätuuleen (siniset käyrät) ja tyvenessä (musta käyrä). Vastatuuleen mennessä kastuminen vähenee nopeuden kasvaessa, myötätuuleen mennessä kastuminen on minimissään tuulen nopeudella edetessä, paitsi $0{,}5\; m/s$ tuulella.

Mutta entä se tilanne tuossa kuvan 5 oikeassa laidassa. Eli myötätuulessa kastuminen on aina minimissään edetessä tuulen nopeudella? Nuo minimithän näkyvät myös kuvassa 6.

Tietyllä ehdolla kyllä, mutta ei aina. Riippuu kokonaistilanteen tarkastelusta. Ajattele vaikka tilannetta hyvin heikolla myötätuulella, eli sataa todella pienessä kulmassa takaviistosta. Jos tällöin kävelisit sateen mukana eteenpäin tuulen mukana hyvin hitaasti, niin etu- ja takaosasi säilyisi kuivana — mutta kastuisit reippaasti yläosastasi, koska matka kestäisi niin kauan.

Eli sen vuoksi tuolla heikoimman myötätuulen käyrällä ei ole minimiä?

Juuri niin. Riippuu tuulen voimakkuudesta kannattaako mennä tuulen mukana vai juosta niin lujaa kuin pääsee. Kastumisen lausekkeesta saadaan ehto

tuulen mukana kävelemiselle. Toisin sanoen, kävely tuulen mukana kannattaa, mikäli paikallaan seisoessa

Vuo takaosan läpi puolestaan on verrannollinen tuulen voimakkuuteen. Meidän esimerkkiparametriemme arvoilla (pinta-alat ja sateen nopeuden pystysuora komponentti) tämä tarkoittaa tuulen nopeutta $v_x>0{,}93\; m/s$. Ehdon toteutuessa kannattaa mennä tuulen nopeudella, muussa tapauksessa aina juosta. Juuri tämän vuoksi kuvassa 6 myötätuulen arvolla $0{,}5\; m/s$ kannattaa juosta (ehto ei toteudu), mutta myötätuulen arvolla $1{,}0\; m/s$ kannattaa kävellä tuulen mukana (ehto toteutuu).

Oho, aika jännä tulos.

Kyllä, etenkin suhteessa siihen kuinka yksinkertaista mallia käytimme. Mutta kuten kaikki kiehtovat arjen ilmiöt, tässäkin ilmiössä riittää hiusten halkomista:

• Ihminen ei ole muodoltaan suorakulmainen särmiö ja raajat liikkuvat eri tavoin kuin keskivartalo.

• Oikea tilanne on kolmeulotteinen ja usein tuulee myös sivulta. 

• Vesipisaroilla on koko- ja nopeusjakauma eikä yhtä tiettyä nopeutta.

• Tuulen nopeus on pienempi lähempänä maata ja se on usein puuskaista.

• Ihon lämpötila höyrystää vettä, mikä osaltaan vähentää veden määrää vaatteissa perille päästyä.

• Vesi saattaa roiskua lahkeille enemmän juostessa kuin kävellessä

• Kehon liike vaikuttaa ilmavirtauksiin ja ilman mukana kulkevien pisaroiden liikkeeseen.

• …Ja niin edelleen ja niin edelleen.

Harvoin on myöskään riittävän tarkkaa tietoa pinta-aloista, tuulen ja sateen nopeuksista ja mahdollisuudesta edellä esitetyn ehdon toteutumiseen. Mallimme ei siten todellakaan ole viimeinen sana juoksemisen kannattavuudesta — aiheesta tehdään tieteellisiä julkaisuja vielä tänäkin päivänä! Mutta jos olet epävarma kannattaako sateessa juosta vai kävellä — varminta on juosta!