Kalajoella länsirannikolla asuva serkkuni sanoi, että oli kerran alkukesällä nähnyt rannalta Ruotsin rannikon. Google Mapsin mukaan Ruotsin rannikko on tasan 100 kilometrin etäisyydellä Kalajoelta. Mutta eihän 100 km päähän voi nähdä..?

Jaa-a, enpä osaa sanoa suoraan, joten pohditaanpa yhdessä. Kun katsot kauas horisonttiin, niin katsot maapallon pyöreän pallopinnan tangentin suuntaan. Koska maapallo on lähes täydellinen pallo, katsoessasi kauas tulee jossain vaiheessa mahdotonta nähdä kaukana olevia kohteita, koska maapallon kaareutuessa Maan pinta estää näkyvyyden. Mitä korkeammalla maanpinnasta ollaan, sitä kauemmas voi nähdä.

No kuinka kauas sitten voi nähdä?

Tutkitaan asiaa kuvan avulla, sillä piirtäminenhän on aina ensimmäinen asia, jonka fyysikko tekee ongelmaa ratkaistessaan.

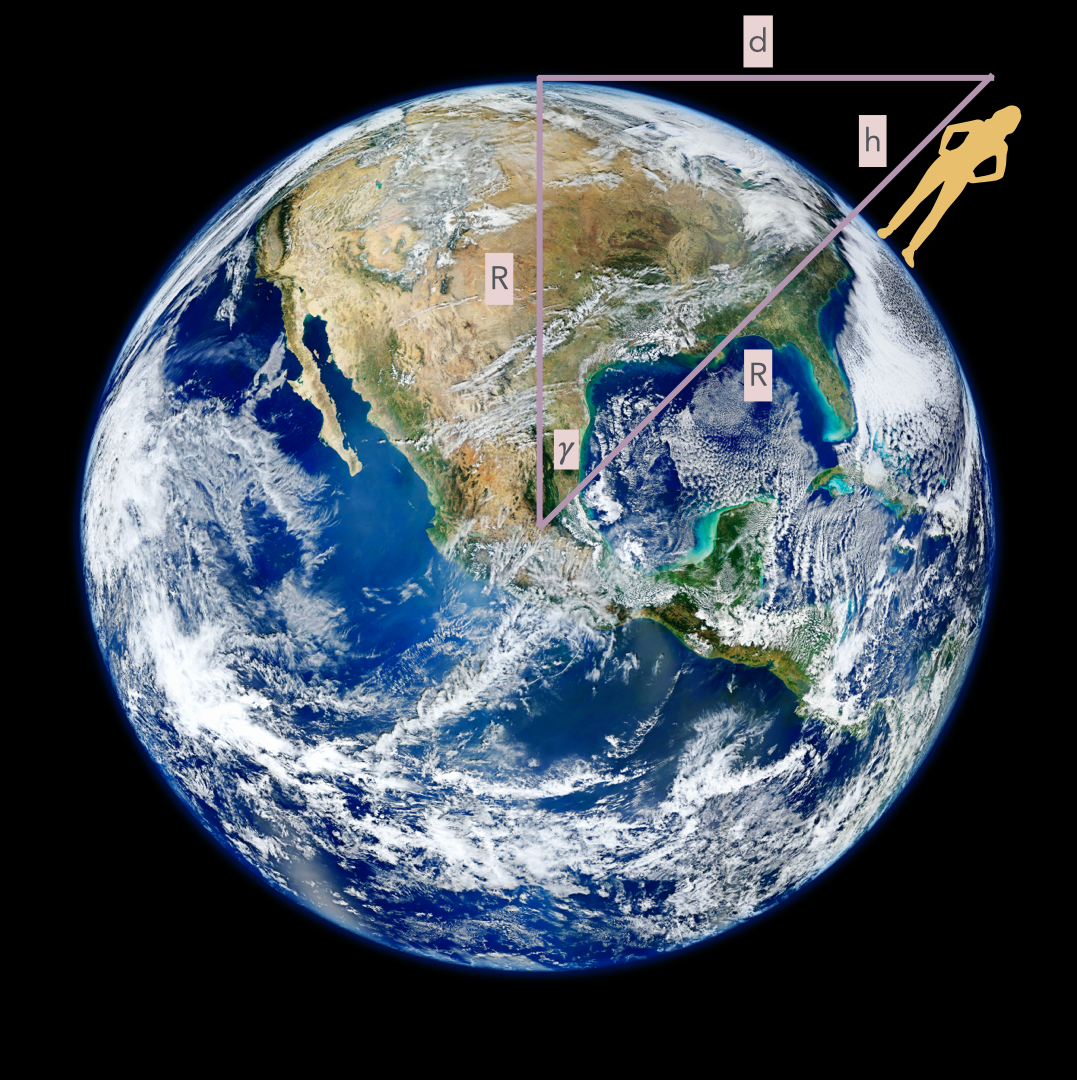
Kuva 1: Suurin mahdollinen katseluetäisyys maanpinnalla. 

Tässä kuvassa katsojan silmät ovat korkeudella $h$ merenpinnasta. $R$ on maapallon säde, joka on $R \approx 6370\;km$. Suurin mahdollinen etäisyys, jonka voi nähdä merenpinnan tasolla on $d$. Tämä on siis matka katsojasta horisonttiin ja juuri se matka jonka haluamme selvittää. Tässä on tärkeää huomata, että teemme sellaisen oletuksen, että valo etenee suoraviivaisesti (tämä on tärkeää myöhemmin).

Kuvasta voi tunnistaa suorakulmaisen kolmion, jonka hypotenuusa on $R+h$ ja kateetit $R$ sekä $d$. Käytetään Pythagoraan lausetta ja ratkaistaan $d$:

Oletetaan, että katsoja seisoo meren rannalla ja katsoo horisonttiin. Jos katsoja on $170\;cm$ pituinen, ovat hänen silmänsä $h=160\;cm$ korkeudella merenpinnasta. Tehdään nyt fysiikassa yleinen temppu ja arvioidaan suuruusluokkia. Jos katsoja seisoo maanpinnalla, yhtälössä $d=\sqrt{h(2R+h)}$ oleva termi $2R+h$ voidaan arvioida olevan lähes sama kuin pelkkä $2R$.

Ai koska maapallon säde on niin paljon suurempi suhteessa silmien korkeuteen maanpinnasta, niin tuo $h$ voidaan vain jättää pois?

Juuri näin. Näin arvioimalla ja sijoittamalla $R = 6370\;km$ saadaan yhtälö 

missä $d$ on etäisyys horisonttiin ja $h$ on katsojan silmän korkeus maanpinnasta. 

Entä jos merellä on korkea majakka, senhän näkee kauempaakin?

Totta, edellinen arvio päteekin vain horisonttiin merenpinnan tasolla. Koska majakallakin on korkeutta, niin sen voi nähdä horisontin takaa. Suurin etäisyys saadaan suoraviivaisella yleistyksellä edellisestä arviosta, eli 

$d\sim 3{,}6\; km (\sqrt{(h/m)}+ \sqrt{(H/m)})$, 

missä $H$ on majakan tai muun asian korkeus. Kuvasta 2 voidaan lukea tarkastelukorkeudesta riippuva horisontin etäisyys.

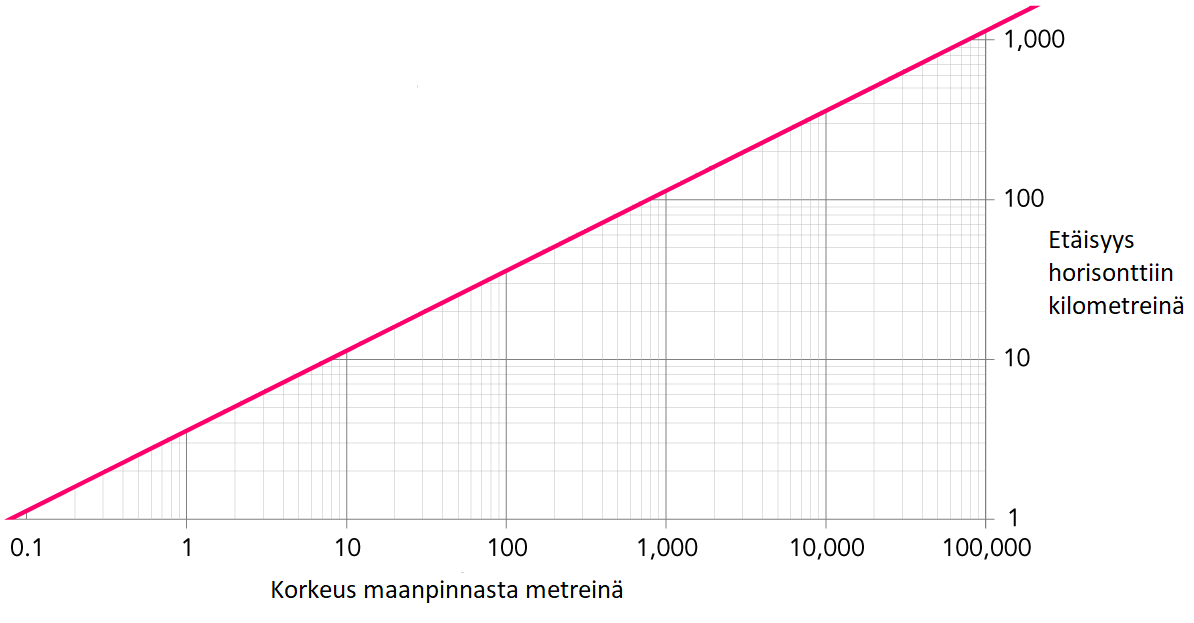
Kuva 2: Tarkastelukorkeudesta riippuva horisontin etäisyys. Kuvan lähde: Wikipedia / Citynoise.

Luenko tuota kuvaa oikein? 100 kilometrin päähän näkemiseen pitäisi olla 800 metrin korkeudella maanpinnasta! Eli serkku puhui palturia…

Ei välttämättä, sillä edellä oletimme valon etenevän suoraviivaisesti. Mutta entä jos oletus onkin väärä?

Ai, että valo mutkittelisi matkalla Ruotsin rannikolta Kalajoelle mennessään?

Juuri niin! Mutkittelu on ihan osuva termi, mutta fysiikassa puhutaan valon taittumisesta. Kaikilla läpinäkyvillä aineilla on taitekerroin $n$, joka kertoo valon nopeuden $v$ aineen sisällä,

missä $c$ on valonnopeus tyhjiössä. Joskus puhutaan myös optisesta tiheydestä; suuremmalla taitekertoimella aine on optisesti tiheämpää. Optisesti tiheämmässä aineessa valo etenee hitaampaa kuin tyhjiössä. Taitekertoimet ovat tyypillisesti luokkaa $n=1\ldots 2$, kaasuille $n\approx 1$, vedelle $n=1{,}33$ ja lasille $n\approx 1{,}5$. Kun valo etenee optisesti tiheämmästä aineesta harvempaan tai harvemmasta tiheämpään, se taittuu. Tyypillinen esimerkki tästä on valon kulkeminen linsseissä, joissa valo kulkee ilmasta lasiin ja takaisin, fokusoituen tai hajaantuen taittumisen seurauksena.

Tai taittuminen uima-altaan vedenpinnasta. 

Juuri niin. Kun valo tulee kahden aineen rajapintaan, taittuminen riippuu tuleeko valo optisesti tiheämmästä optisesti harvempaan aineeseen vai toisin päin. Kuvassa 2 valo tulee aineesta A aineeseen B ja taittuu. Valon tulokulma on $\alpha$ ja taitekulma $\beta$. Kulmat mitataan suhteessa pinnan normaaliin eli rajapintaa vasten kohtisuoraan suuntaan.

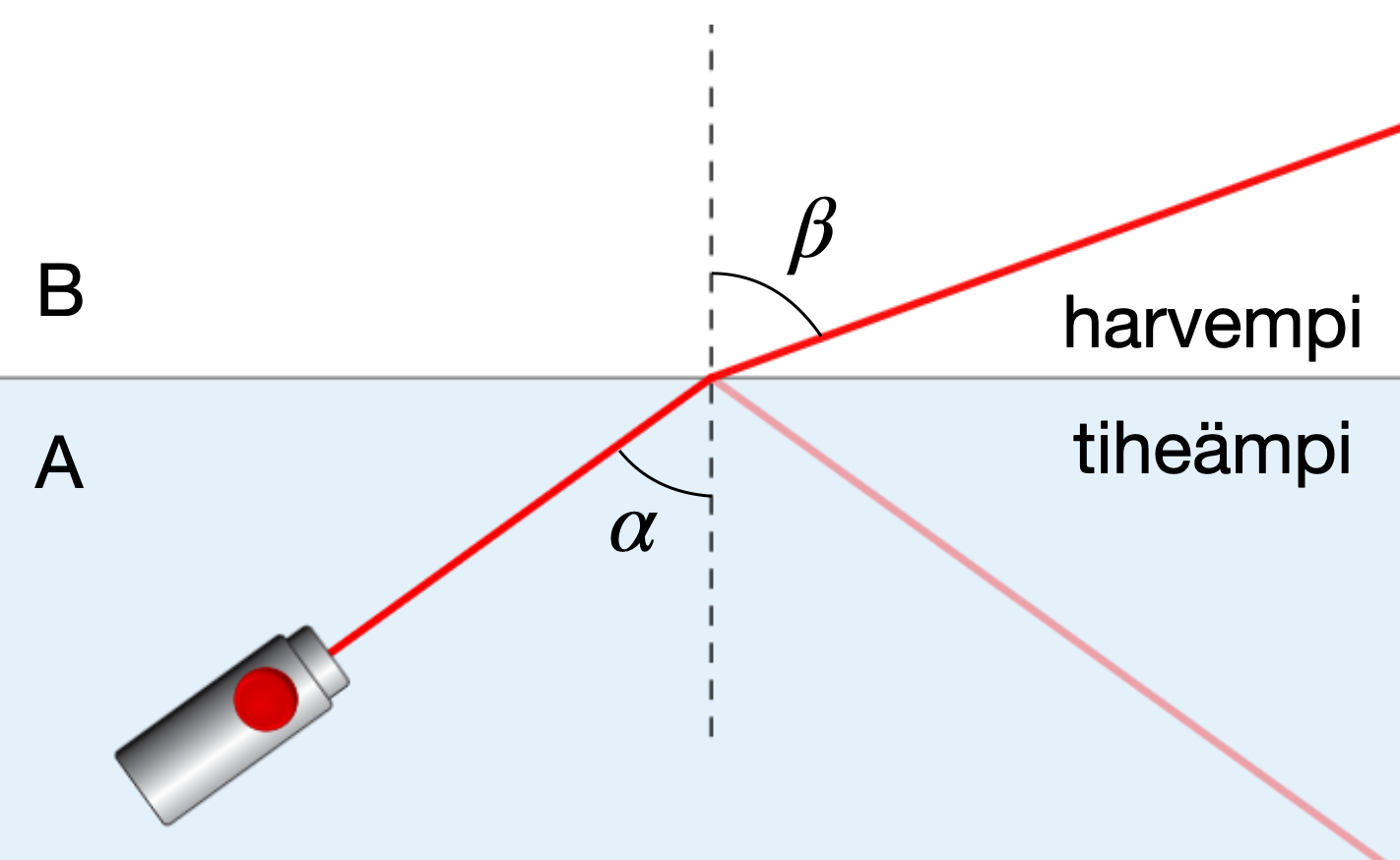
Kuva 3: Valon taittuminen kahden aineen rajapinnassa.

Koska aine B on optisesti harvempaa kuin aine A, niin $\beta > \alpha$ eli valo taittuu normaalista pois päin. Aine A voisi olla esimerkiksi vettä ja aine B ilmaa. Valon tulo- ja taitekulmien mittaamisella saisimme selville taitekertoimet käyttäen Snellin lakia, jonka mukaan

Snellin laki voidaan perustella Fermat’n periaatteen avulla. Periaatteen mukaan valo kulkee pisteestä toiseen aina nopeinta reittiä pitkin. Valon taipuminen kahden aineen rajapinnassa voidaan ymmärtää tämän periaatteen avulla: valo taittuu kahden aineen rajapinnassa siten, että valon kulkee matkansa mahdollisimman nopeasti. Vertaa periaatetta vaikka tilanteeseen, jossa rannalla seisova hengenpelastaja näkee pelastettavan meressä, hieman rannan suuntaan oikealla. Pelastajan kannattaa juosta pidempi matka rannalla ($\approx$ pieni taitekerroin ja suuri nopeus) ja uida lyhyempi matka vedessä ($\approx$ suuri taitekerroin ja pieni nopeus). Näin nopeinta reittiä seuratessa hengenpelastajan kulkusuunta muuttuu rannalta veteen siirryttäessä. Voit itse kokeilla asiaa tämän simulaation avulla.

Toisaalta kuvan 3 avulla voidaan pohtia mitä tapahtuu kulman $\alpha$ kasvaessa. Koska $\beta > \alpha$, niin on olemassa kulma $\alpha'$, jolloin $\beta = 90^\circ$ ja osa valosta ei enää taitu rajapinnassa vaan kaikki valo heijastuu. Tätä ilmiötä kutsutaan kokonaisheijastumiseksi. Snellin lain perusteella rajakulma toteuttaa yhtälön 

Kokonaisheijastus voi tapahtua vain kun valo etenee optisesti tiheämmästä aineesta harvempaan (Video 1). 

Video 1: Kokonaisheijastuminen tapahtuu valon mennessä tiheämmästä aineesta harvempaan, kun tulokulma on riittävän suuri. Alemman aineen taitekerroin in $1{,}05$ ja ylemmän aineen taitekerroin on $1{,}0$.

Voit itse kokeilla videon simulaatiota täällä.

Ja tämä liittyy Ruotsin rannikon näkemiseen?

Okei, siirrytään teoriasta käytäntöön. Meren yllä olevassa ilmassa on erilämpöisiä kerroksia. Varsinkin keväällä tai alkukesästä merivesi voi olla huomattavasti viileämpää kuin ilma. Tällöin ilma meren yllä on viileää ja korkeammalla lämpimämpää. Näiden kahden erilämpöisen ilman raja saattaa olla hyvinkin selvä ja lämpötila muuttuu viileästä lämpimäksi lyhyellä korkeuserolla.

Lämmin ilma on kylmää ilmaa harvempaa, minkä voi ymmärtää vaikka ideaalikaasulain

avulla, missä $\eta=N/V$ on kaasun hiukkastiheys, $p$ paine, $k_B$ Boltzmannin vakio ja $T$ lämpötila.  Kaasujen taitekerroin on suoraan verrannollinen tiheyteen,

jolloin kaasujen taitekerroin kasvaa tiheyden kasvaessa eli lämpötilan pienentyessä. Tämän verrannollisuuden vuoksi ilma merenpinnan yllä on optisesti tiheämpää ja ilma korkeammalla optisesti harvempaa. Tämä näkymätön rajapinta voi aiheuttaa meren yllä yhden tai useamman kokonaisheijastuksen (Kuva 4).


Kuva 4. Kylmästä, tiheästä ilmasta yläviistoon kulkeva valo voi kokonaisheijastua ja kääntyä kulkemaan alaviistoon.

Näin ollen Ruotsin puolelta yläviistoon suuntautuva pääsee ikään kuin kiertämään Maapallon kaarevuuden mukana. Siksi horisontin yllä on mahdollista nähdä kaukainen heijastus Ruotsin rannikosta! Tästä todistaa myös kuva 5. 

Kuva 5: Ruotsin rannikko Selkämeren yli kuvattuna. Kuva: Heikki Salokangas/SAKL

Eli serkkuni havainto saattoi olla kuin ollakin todellinen.

Kyllä vain. Sama ilmiö on kyseessä kangastuksissa, joita yleensä nähdään aavikoilla tai kuumina päivinä asfaltin pinnoilla. Näissä kangatuksissa lämpötilaero on toisin päin: ilman maan pinnalla on auringonpaisteesta kuumaa ja harvaa, samalla kun ilma korkeammalla on viileää ja tiheää. Tällöin alaviistoon kulkeva valo kokonaisheijastuu kulkemaan yläviistoon, jolloin tien pintaa katsoessa nähdäänkin taivasta — mikä erehdyttävästi näyttää vesilätäköltä! (Kuva 6).

Kuva 6: Kuuman asfaltin pinnalta kangastuu taivas.