Voisiko jalkapalloa potkaista kierteellä niin, että se tulisi takaisin kuin bumerangi?
Katselin eilen YouTube-videoita ja näin maalin, jota on kutsuttu kaikkien aikojen vapaapotkumaaliksi jalkapallossa.
Video 1: Roberto Carlosin vapaapotkumaali.
Olipa kyllä uskomaton laaki!
Joo, mutta miten tuollainen potku on ylipäänsä mahdollista? Pallo oli menossa ensin ohi maalin mutta sitten suunta kääntyikin kohti maalia. Ihan kuin lennon aikana palloon vaikuttaisi ihan itsestään sen liikesuuntaa muuttava voima.
Kierrepotkut ovat tosiaan mielenkiintoisia ja niitä on tutkittukin intensiivisesti. Onhan ilmiö kiintoisa suurelle määrälle ihmisiä, sillä jalkapallo on maailman suosituin urheilulaji.
Tartunpa kiinni tuohon sun käyttämään sanaan “voima”. Mitä ajattelet: mitä voimia jalkapalloon vaikuttaa kierrepotkun jälkeen, kun se lentää ilmassa?
Voimista onkin puhuttu fysiikan tunneilla.
Okei, mutta eiväthän nuo painovoima ja ilmanvastus selitä sitä kierrettä. Täytyy olla siis muitakin voimia.
Joo, on tosiaan vielä eräs palloon vaikuttava voima: Magnuksen voima. Nimensä voima on saanut sitä 1800-luvulla tutkineelta saksalaiselta tutkijalta Heinrich Gustav Magnukselta. Jotta ymmärtäisimme Magnuksen ilmiötä, täytyy meidän ensin puhua Bernoullin periaatteesta.
Virtausmekaniikkaa 1700-luvulla tutkinaan sveitsiläisen matemaatikon ja fyysikon Daniel Bernoullin mukaan nimetyn periaatteen mukaan virtaavan fluidin (nesteen tai kaasun) paine laskee virtausnopeuden kasvaessa. Bernoullin periaate liittyy energian säilymiseen: jos fluidiin ei tuoda energiaa ulkopuolella, sen kokonaisenergian täytyy säilyä. Koska fluidin virtausnopeuden kasvu nostaa liike-energiaa, täytyy samalla sisäisen energian (mukaan lukien lämpöliike) ja potentiaalienergian laskea. Tämä ilmenee fluidin paineen laskuna. Teknisesti ilmaistuna, suure
ei muutu, kun seuraamme virtausta mukailevaa virtaviivaa. Lausekkeessa  on fluidin tiheys,
on fluidin tiheys,  virtausnopeus ja
virtausnopeus ja  paine (lauseke olettaa korkeusmuutosten olevan pieniä). Bernoullin periaate tulee ottaa huomioon kaikenlaisten kaasujen ja nesteiden virtauksia tutkittaessa.
paine (lauseke olettaa korkeusmuutosten olevan pieniä). Bernoullin periaate tulee ottaa huomioon kaikenlaisten kaasujen ja nesteiden virtauksia tutkittaessa.
Sen sijaan Magnuksen ilmiö ja siihen liittyvä voima vaikuttaa tilanteissa, jossa kappale (kuten jalkapallo) etenee nesteen tai kaasun (kuten ilman) läpi ja samalla pyörii itsensä ympäri. Magnuksen ilmiö aiheutuu ilman vuorovaikutuksesta kappaleen pinnan kanssa.
Tutkitaan nyt jalkapallon etenemistä ilmassa. Olkoon pallolla vaikka yläkierrettä (Kuva 1). Yläkierre tarkoittaa sitä, että pallo pyörii etenemissuuntaansa nähden siten, että pallon yläosa pyörii kohti etenemissuuntaa.
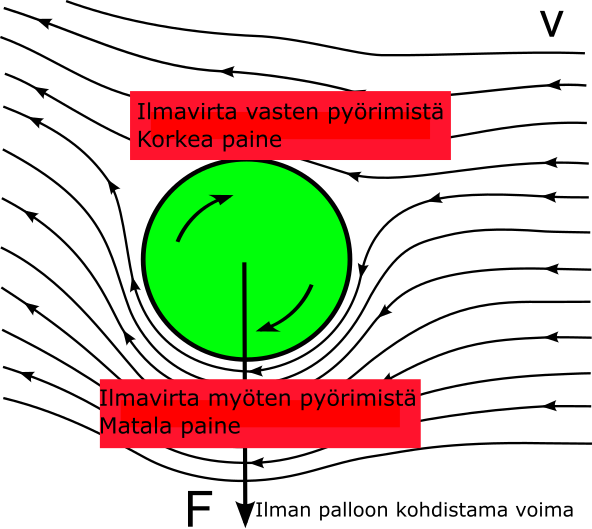
Kuva 1: Magnuksen voima, kun pallo kulkee oikealle yläkierteellä. Kuvaa on muokattu alkuperäisestä.
Pallon pinta ei ole täysin tasainen ja siispä pallon pinnan ja ilman välillä on kitkaa. Kitkan vaikutuksesta pallon alapuolella ilma virtaa pallon pyörimisen mukana pallon taakse ja ylöspäin ja virtausnopeus kasvaa. Samaan aikaan pallon yläpuolella pyöriminen vastustaa ilman liikettä ja virtausnopeus hidastuu.
Kun pallon yläpuolella virtausnopeus on pienempi ja alapuolella suurempi, niin Bernoullin periaatteen mukaan pallon yläpuolella paine on suurempi kuin alapuolella. Tämän paine-eron vuoksi ilma kohdistaa tällöin palloon voiman alaspäin. Tämä on Magnuksen voima, joka aiheuttaa pallon kierteen. Vastaava pätee myös alakierteelle (voima kohdistuu ylöspäin) tai sivukierteelle (voima pallon etenemissuuntaan nähden jommalle kummalle sivulle).
Testaa kotona Magnuksen ilmiötä
Tarvikkeet: A4 -paperiarkki, jonkinlainen ramppi (esim. iso kirja tai lauta)
Ohjeet:
-
Tee paperiarkista lieriö
-
Ota ramppi ja pidä sitä ilmassa pienessä kulmassa maan suhteen.
-
Aseta paperilieriö rampin yläosaan ja anna sen pyöriä vapaasti alas ja pudota. Miten lieriö putoaa?
-
Miten selittäisit liikkeen?
Testauksesi tulos voi näyttää esimerkiksi tältä.
Video 2: Magnuksen ilmiön demonstraatio.
Okei, eli siis pallon pyöriminen saa aikaan sen kierteen tuon Magnuksen ilmiön kautta ja tämä johtuu ilman ja pallon pinnan välisestä kitkasta.
Juuri näin. Kuitenkin ilma voi käyttäytyä pallon pinnalla myös eri tavalla. Lienet kuullut turbulenssista?
Kerran lentokoneessa kuulutettiin, että on turbulenssia. Sitten lentokone tärisi ja heittelehti aika voimakkaasti.
Jos katsotaan tuota edellistä kuvaa Magnuksen ilmiön kohdalla, niin siinä ilma virtasi tasaisesti rinnakkaisissa kerroksissa. Sellaista virtausta kutsutaan laminaariseksi virtaukseksi. Turbulentissa virtauksessa sen sijaan ilmavirtauksessa on äkkinäisiä ja satunnaiselta vaikuttavia muutoksia. Joskus lentokone päätyy alueelle, jossa ilma virtaa turbulenttisesti tai virtaus siiven suhteen muuttuu turbulentiksi. Tällöin lentokone heittelehtii voimakkaasti.
Virtauksen laminaarisuuteen tai turbulenttiuteen vaikuttaa moni tekijä. Jalkapallon tapauksessa se riippuu erityisesti siitä, miten nopeasti pallo lentää ilmassa. Kun pallo lentää riittävän nopeasti, ilma käyttäytyy turbulenttisesti. Nopeuden ollessa riittävän hidas, ilma käyttäytyy lähinnä laminaarisesti. Turbulenttisuutta voi arvioida dimensiottoman Reynoldsin luvun
avulla. Lausekkeessa  on fluidin virtausnopeus,
on fluidin virtausnopeus,  kappaletta luonnehtiva pituus (esimerkiksi pallon halkaisija) ja
kappaletta luonnehtiva pituus (esimerkiksi pallon halkaisija) ja  fluidin kinemaattinen viskositeetti. Kun Re on pieni, virtaus on laminaarista, kun Re on suuri, virtaus on turbulenttista; tarkat numeeriset raja-arvot riippuvat geometriasta ja kappaleen pintamateriaalista.
fluidin kinemaattinen viskositeetti. Kun Re on pieni, virtaus on laminaarista, kun Re on suuri, virtaus on turbulenttista; tarkat numeeriset raja-arvot riippuvat geometriasta ja kappaleen pintamateriaalista.
Onko sillä väliä pallon liikkeen kannalta, liikkuuko ilma laminaarisesti vai turbulenttisesti?
Sillä on itse asiassa paljon merkitystä. Pallon ilmanvastus on laminaarisella virtauksella jopa kaksi kertaa suurempi kuin turbulentilla! Tämä käy järkeen, jos ajattelee kitkaa ilmanvastuksen analogiana: laminaarisen virtauksen tapauksessa pallo ikään kuin hankaa ilmaa, ilma kohdistaa palloon suuren voiman. Turbulentin virtauksen tapauksessa tätä hankausta esiintyy vähemmän. Tällä on erityisesti merkitystä turbulentin ja laminaarisen ilmavirtauksen rajalla.
Tällöin varmaan peleissä syntyisi enemmän maaleja, jos voitaisiin jotenkin kontrolloida, että pallojen lento olisi mahdollisimman pitkään turbulenttista, koska tällöin pallot lentäisivät mahdollisimman nopeasti.
Itse asiassa kaikkein haastavinta maalivahdeille on juuri se taitekohta, jolloin ilma alkaa virrata laminaarisesti, sillä tällöin pallon liike on vähiten ennalta-arvattavaa. Tätä taitekohtaa voidaan kontrolloida pallon pinnan muotoilulla ja saumojen sijoittelulla. Yleensä ottaen pinnan epätasaisuus, nyppylät ja saumat pienentävät sitä rajanopeutta jolloin ilmavirta alkaa virrata laminaarisesti.
Pallossa olevista nyppylöistä tulee mieleen golf-pallot!
Olet oikeassa, golf-pallon pinta on täynnä kuoppia juuri tämän takia. Kuoppien ansioista golf-pallon ympärillä on turbulenttinen ilmavirtaus ja täten ilmanvastus on pienempi. Testien perusteella tiedetään, että golf-pallon kuopat saavat sen lentämään kaksi kertaa kauemmas verrattuna muuten samanlaiseen palloon ilman kuoppia!

Kuva 2: Golf-pallon pinnalla on 300 - 450 kuoppaa.
Vuonna 2010 jalkapallon MM-kisoissa kohdattiin fiasko, kun moni pelaaja kritisoi kisojen virallista pelipalloa, Jabulania. Näissä kisoissa oli useammin laukauksia, joissa taitekohta tapahtui juuri ennen maalivahdin torjuntaa, jolloin laukauksen lentorata muuttui yllättävästi. Tutkimuksissa paljastui, että pallo oli sileämpi verrattuna muihin yleisesti käytettyihin palloihin. Täten ilmavirta alkoi käyttäytyä laminaarisesti suuremmilla nopeuksilla kuin yleensä, ja pallo hidastui nopeammin. Kuva 3 vertailee Jabulania toiseen jalkapalloon (Brazuca). Jabulanin ilmanvastuskertoimen muutos tapahtuu noin  suuremmassa nopeudessa kuin Brazucan. Videossa 3 näet myös itse Jabulanin käyttäytymistä.
suuremmassa nopeudessa kuin Brazucan. Videossa 3 näet myös itse Jabulanin käyttäytymistä.
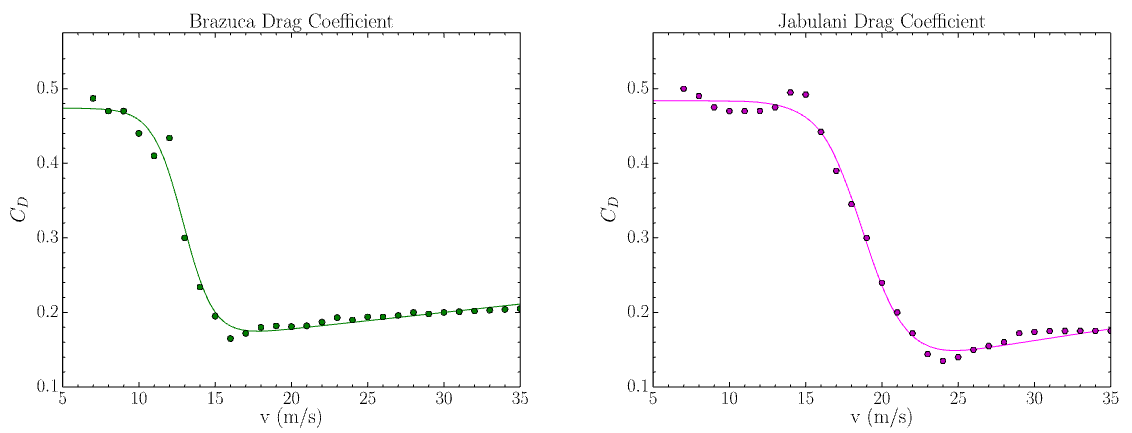
Kuva 3: Jabulanin ja toisen jalkapallon ilmanvastuskerroin sen liikenopeuden funktiona. Lähde: https://iopscience.iop.org/article/10.1088/1361-6404/aaa888/pdf.
Video 3: Jabulanin liikehdintää.
Kaiken lisäksi lentävä pallo voi kokea myös ns. käänteisen Magnuksen ilmiön. Käänteinen Magnuksen ilmiö aiheutuu siitä, että pallon toisella puolella ilma virtaa laminaarisesti ja toisella puolella turbulenttisesti. Tällöin ilman ja pallon vuorovaikutuksessa voima kohdistuukin päinvastaiseen suuntaan kuin Magnuksen ilmiössä.
Käänteinen Magnuksen ilmiö esiintyy vain palloilla, jotka ovat pinnaltaan riittävän sileitä, kuten aiemmin esillä ollut Jabulani-jalkapallo. Sen voi nähdä helpommin potkaistaessa rantapalloa, joka on pinnaltaan hyvin sileä.
Kaiken kaikkiaan pallon lentoradan mallintaminen on monimutkaista. Lisäksi siihen vaikuttavat paikalliset olosuhteet, sillä ilman kohdistamiin voimiin vaikuttaa myös ilman tiheys.
Onpa kiinnostavaa! Minulla on vielä yksi kysymys, kun olemme puhuneet näistä kierteistä niin paljon. Olisiko mahdollista potkaista palloa sellaisella kierteellä, että se palaisi takaisin kuin bumerangi?
Periaatteessa kyllä, käytännössä ei. Pallo tulisi potkaista niin, että se pyörisi erittäin voimakkaasti, mutta kuitenkin kulkisi riittävän hitaasti eteenpäin, jottei sen tarvitsisi palata takaisin niin pitkää matkaa. Jos sitä ei kuitenkaan potkaise riittävän nopeasti, se putoaa liian nopeasti. Mietitään sitä ensimmäistä vapaapotkumaalia, jonka näytit. Pallo potkaistiin 35 metrin etäisyydeltä maalista. Jotta pallo kävisi 35 metrin päässä ja tulisi takaisin, pallon lähtönopeuden tulisi olla noin  . Suurimmissa mitatuissa lähtönopeuksissa jalkapallon nopeus on ollut noin
. Suurimmissa mitatuissa lähtönopeuksissa jalkapallon nopeus on ollut noin  .
.
Jos siis haluat pallon palaavan takaisin, kannattaa potkaista pallo suoraan ylöspäin — tai vastatuuleen.
| Tiivistelmä |
| Pallon kierre johtuu sen pyörimisestä ilmassa. |
| Pyörimisen ansio ilmanpaine pallon eri puolilla vaihtelee ja tämä saa aikaan voiman. |
| Bumerangimaiseen potkuun pallo pitäisi potkaista monta kertaa suurempaan vauhtiin kun mitä käytännössä on mahdollista. |


