Eilen kun kävin kuntosalilla, testasin etukyykkyä ja jaksoin nostaa paljon takakyykkyä vähemmän rautaa. Miksi näin on, kun molemmissa liikkeissä kuitenkin mennään painon kanssa kyykkyyn ja noustaan ylös olennaisesti samalla tavalla?

Lyhyesti vastattuna, kuormituksen tunne ei ensisijaisesti liity painoon, vaan voiman vääntömomentteihin eri nivelten suhteen. 

Pohditaan tätä rauhassa ja vaiheittain. Ensinnäkin, muistatko mikä ero on massalla ja painolla?

No ainakin ihminen on eripainoinen Kuussa, vaikka massa on sama.

Tuon muistaminen auttaa oikeille jäljille. Maan pinnalla olevaan  $m$-massaiseen kappaleeseen kohdistuu alaspäin kohdistuva painovoima eli gravitaatiovoima, jonka suuruus on $G=mg$ missä vakiota $g=9{,}81\;m/s^2$ kutsutaan Maan putoamiskiihtyvyydeksi. Kuussa tilanne on sama, mutta putoamiskiihtyvyyden arvo $1{,}63\; m/s^2$, joten myös painovoima on pienempi. Aivan kuten muistelit. Painovoima syntyy siitä, että kaikkien massakappaleiden välillä on vetovoima; maassa on enemmän massaa, joten maan aiheuttama voima maan päälliseen kappaleeseen on suurempi. Massa on kappaleen sisäinen ominaisuus; paino riippuu tilanteesta. Esimerkiksi vuoristoradassa paino aiheutuu sekä gravitaatiosta että vaihtelevasta kiihtyvyydestä. Alaspäin kiihtyvässä hississä paino on hetkellisesti pienempi, ylöspäin kiihtyvässä hississä suurempi.

Newtonin I lain mukaan kappaleen liiketila ei muutu, mikäli kappaleeseen kohdistuvien voimien summa on nolla. Levytanko säilyy levossa, kun siihen kohdistuu painovoiman lisäksi lattian kohdistama tukivoima ylöspäin siten, että voimien summa on nolla (Kuva 1).

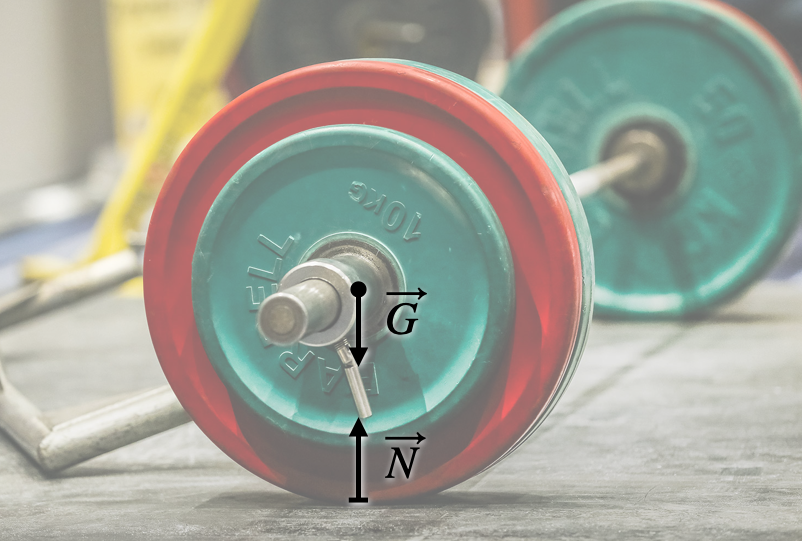
Kuva 1. Levytankoon kohdistuvat voimat tangon ollessa levossa.

No tietty. Maassa on tietty painovoima ja kuussa on sitten eri eri painovoima, kun sen massa on eri suuruinen, kuten juuri kerroit.

Painovoima eri puolilla maapalloa on usein sama riittävällä tarkkuudella, mutta täsmälleen sama se ei ole. Nimittäin, putoamiskiihtyvyys vaihtelee sijainnista riippuen maapallon pyörimisen, oblaatin eli littanan muodon (joka sekin on seurausta pyörimisestä) sekä pienempien paikallisten vaihteluiden kuten maankuoren koostumuksen vuoksi. Äärimmillään putoamiskiihtyvyys vaihtelee arvosta $9{,}7639\; m/s^2$ (Huascarán vuori, Peru) arvoon $9{,}8337\;m/s^2$ (Jäämeri); suurimmillaan vaihtelu on siis jopa $0{,}7$ %, eli lähes prosentin verran! Esimerkiksi Jyväskylässä $g=9{,}8205\; m/s^2$ ja Singaporessa $g=9{,}7806\; m/s^2$. Siten $250$ kilogramman paino on Jyväskylässä $2455$ Newtonia ja Singaporessa $2445$ Newtonia, eli $10$ Newtonia vähemmän. Näin $250$ kilon nostaja nostaisi Singaporessa efektiivisesti yli kilogramman verran vähemmän kuin Jyväskylässä!

Täh?! Ei voi olla — muutoinhan maailmanennätyksetkin riippuisivat siitä missä niitä nostetaan.

Aivan! Niin ne riippuvatkin, vaikka eihän sellaisesta puhuta. Kuitenkin levypainoista vakioidaan massa, ei paino, koska tällöin painoja saisi käyttää vain tietyssä paikassa (tai paikassa, jossa on tietty $g$:n arvo). Merkitys on havaittava, mutta ehkä se koetaan niin pieneksi, että suurta yleisöä ei haluta “häiritä” moisilla todellisuuden yksityiskohdilla…

Onneksi tärkeimmät kilpailut sentään käydään normaalisti samassa paikassa, jolloin kaikilla toisiaan vastaan kilpailevilla on ainakin sama painovoima. Tosin tässäkin poikkeus vahvistaa säännön: korona-aikana oli myös kilpailuja, jotka tapahtuivat samanaikaisesti eri puolella maapalloa. Tällöin maantieteellisesti pienen $g$:n alueen kilpailijoilla oli aito kilpailuetu muihin verrattuna.

Aika yllättävää.

Jokseenkin kyllä. Mutta jatketaan alkuperäistä tarkasteluamme. Levytanko lähtee nousemaan ylöspäin, mikäli sen kiihtyvyys $\vec{a}$ on hetkellisesti ylöspäin. Kiihtyvyys määräytyy Newtonin II laista

massan $m$ ja massaan kohdistuvien voimien $\vec{F}_i$ summan mukaisesti. Jos siis haluat nostaa $100$ kg:n levytangon, sinun on kohdistettava tankoon ylöspäin suuntautuva voima, jonka suuruus on vähintään $981$ Newtonia. Käytännössä tankoon kohdistuva voima voi olla hetkellisesti kymmeniä prosentteja tätä suurempi; ilman kohtuullista kiihtyvyyttä tanko liikkuisi ylöspäin tuskallisen hitaasti. Esimerkiksi tasainen $1\; m/s^2\approx g/10$ kiihtyvyys ylöspäin vastaisi tangon nostamista $12\; cm$:n puolessa sekunnissa; tämä kiihtyvyys vaatisi tankoon ylöspäin kohdistuvan voiman, joka on $10$ % sen staattista painoa suurempi.

Okei, eli mekaniikan perusteita. Mutta entä sen nostotekniikan vaikutus?

Hyvä, edetään siis keskustelemaan nostotekniikasta, joka aloitetaan ilmeisellä toteamuksella: mikään lihas ei nosta painoa suoraan, vaan vipujärjestelmän kautta. Vipujen tarkastelussa keskeistä on voimien vääntömomentit eri nivelten suhteen. Vääntömomentti mittaa kappaleeseen kohdustuvan voiman kykyä kiertää kappaletta nivelen eli kiertoakselin suhteen. Voiman $F$ aiheuttama momentti pisteen $p$ suhteen on 

missä $d$ on voiman vipuvarsi eli voiman kuvitteellisen vaikutussuoran lähin etäisyys pisteeseen $p$ (Kuva 2). Mitä pidempi vipuvarsi, sitä suurempi kyky voimalla on aiheuttaa kiertymistä. Pidemmällä vipuvarrella yhtä voimakkaaseen kiertämiseen tarvitaan myös pienempi voima. Jos kappaleen kiertymiseen vaikuttaa useita voimia, kiertymisen määrää voimien vääntömomenttien summa; mikäli summa on nolla, kappale säilyy tasapainossa.

Kuva 2. Voimien $\vec{F}_i$ vääntömomentteja pisteen $p$ suhteen. Tilanteissa 1 ja 2 voiman vääntömomentit ovat yhtä suuria, koska voiman $F_i$ ja vipuvarren tulo on sama ($F_1d_1=F_2d_2$). Tilanteessa 3 voima on suurin, mutta vipuvarsi on nolla, joten vääntömomentti on myös nolla.

Mutta vääntömomentilla on myös suunta riippuen siitä, että kiinnitätkö tai avaatko mutteria.

Niin on. Vääntömomentti on vektorisuure, jolla on suuruus ja suunta. Tässä keskustelussa kuitenkin oiomme hieman, koska täsmällinen vektoreiden käsittely ei nyt ole tarpeen. Sovitaan vaikka, että vääntömomentti on positiivinen kun kierto on ruudun tasossa vastapäivään.

Vipuvarsien vuoksi lihakset ovatkin vahvempia kuin arvaammekaan. Jos esimerkiksi videon 1 käsi pitää $10$ kg:n käsipainoa tasapainossa, kokonaisvääntömomentti $p$:n suhteen täytyy olla nolla ja voimien $F_m$ ja $F_h$ vääntömomenttien täytyy vastakkaismerkkiset mutta yhtä suuret, eli $d_mF_m = d_h F_h$.

Video 1. Lihakset aiheuttavat liikettä vipujärjestelmän kautta. Kyynärpää toimii nivelenä, jonka suhteen kyynärvartta kierretään hauislihaksen (tai ojentajalihasten) avulla.

Mutta kyykkyä ei tehdä hauiksilla.

No ei, joten edetään siis kyykkyyn ja tarkastellaan levytangon painon aiheuttamia vääntömomentteja polvi- ja lonkkanivelten suhteen. Kyykyssä taipuu myös nilkka, mutta sen rooli liittyy lähinnä tasapainon säilyttämiseen, ei painon nostamiseen. Tarkastellaan kolmea kyykkyvariaatiota, low-bar takakyykkyä, high-bar takakyykkyä ja etukyykkyä (Kuva 3). Low-bar takakyykyssä tanko on lapaluun alapuolella, takaolkalihasten päällä, high-bar takakyykyssä epäkäslihaksen päällä lapaluun yläpuolella. Etukyykyssä tankoa pidetään käsillä tuettuna kaulan edessä, olkalihasten päällä.

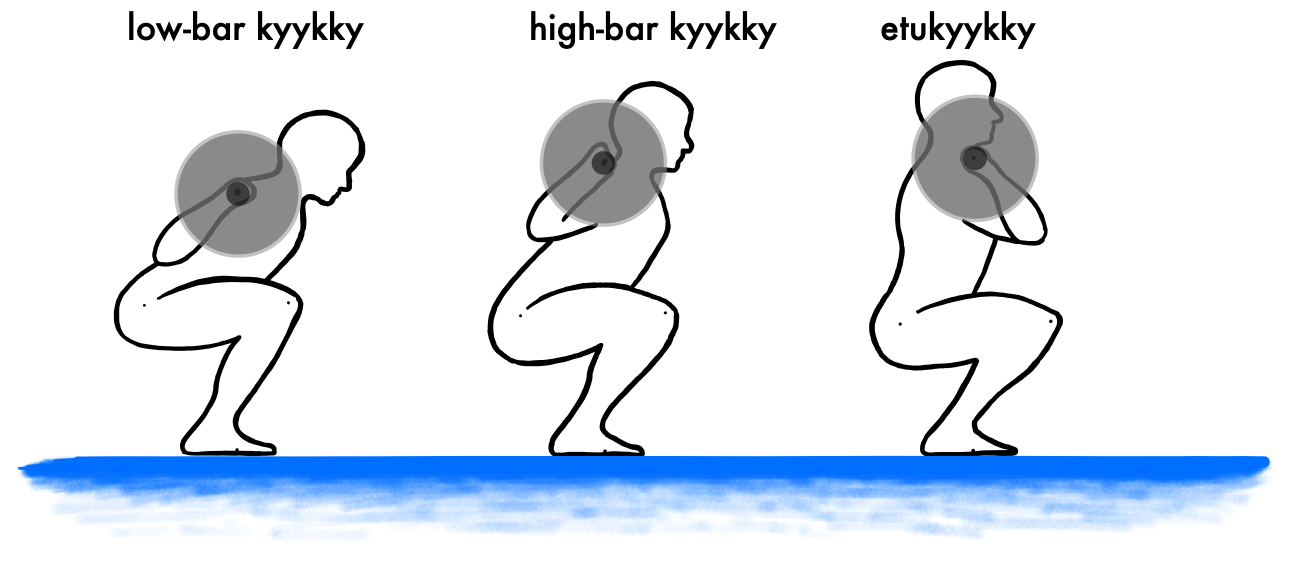
Kuva 3: Jalkakyykyn kolme variaatiota, low-bar -takakyykky, high bar -takakyykky ja etukyykky.

Tarkastellaan vääntömomentteja polven ja lonkan suhteen. Myös keho aiheuttaa vääntömomentteja, mutta keskitytään tässä pelkästään siihen millaiset vääntömomentit levytanko aiheuttaa kullakin tekniikalla kehopainon lisäksi. Alla olevat numeeriset arvot variaatioiden kuvailussa ovat suuntaa-antavia ja riippuvat nostajan tekniikan nyansseista ja kehon mittasuhteista. Tarkastellaan liikkeiden ala-asentoja, koska niissä nivelten kuormitus on suurimmillaan (Kuva 4).

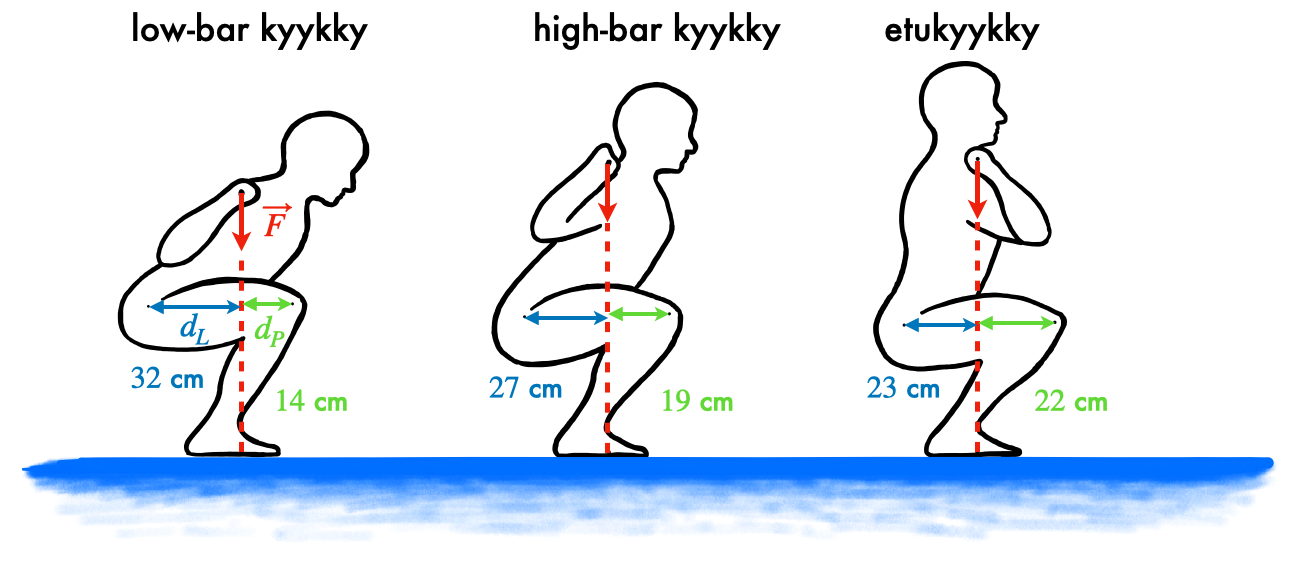
Kuva 4. Levytangon painon vipuvarsien pituudet $d_L$ ja $d_P$ lonkka- ja polvinivelten suhteen eri kyykkyvariaatioissa.

Kuvaan on merkitty katkoviivalla voiman vaikutussuora, jonka avulla voimme mitata vipuvarren $d_L$ lonkkanivelen $L$ suhteen ja vipuvarren $d_P$ polven $P$ suhteen. Lasketaan $100$ kg:n levytangon aiheuttamat vääntömomentit pisteiden $L$ ja $P$ suhteen Taulukkoon 1.

Taulukko 1. Vääntömomentit lonkan ($d_LF$) ja polven ($d_PF$) suhteen $100$ kg:n tangolla kuvassa 4, kun tangon paino on $F=981$ N.

Nyt voisit pureksia noita lukuja yksi kerrallaan.

Low bar -kyykyssä polvinivel on suorempana ja lantiokulma pienempi. Se siis kuormittaa lonkkaniveltä enemmän, polvea vähemmän, mikä näkyy vääntömomenteissa selkeästi.

Entä muuten alaselkä? 

Hyvä huomio. Alaselkä on lähellä lonkkaniveltä, joten lonkan vääntömomentti kuvaa jokseenkin myös alaselän kuormitusta. Low-bar on siten kuormittavampi lantiolle ja alaselälle, mutta keveämpi polvinivelelle. 

Etukyykyssä lonkan vääntömomentti on pienempi, polven vääntömomentti suurempi — aika merkittävästi. Etukyykyssä polvi on ääriasennossa taittuneempi. Siten etukyykky on kuormittavampi polvelle, mutta kevyempi lonkalle ja alaselälle. Tangon vääntömomentti polveen on suurempi kuin takakyykyissä, vaikka tanko on edessä; tämä hieman yllättävä piirre johtuu huomattavasti suoremmasta selästä ja pienemmästä polven nivelkulmasta.

High-bar takakyykky sijoittuu näiltä osin etukyykyn ja low-bar kyykyn väliin.

Mutta entä alkuperäinen kysymys? Miksi sain etukyykyssä ylös paljon vähemmän rautaa? Taulukon mukaan etukyykyssä rasitus lonkan ja polven suhteen on jakaantunut tasaisemmin, joten sen voisi ajatella olevan tehokkain tapa kyykätä.

Rasituksen tasainen jakautuminen olisi hyvä argumentti, mikäli nivelet olisivat samanlaisia. Kuitenkin lonkkanivel on polviniveltä paljon vahvempi. Lonkkaa ojentavat vahvat takaketjun lihakset; polvea ensisijaisesti nelipäinen reisilihas. Siten polveen kohdistuva vääntömomentti kuormittaa reisiä, lonkkaan kohdistuva vääntömomentti pakaroita ja alaselkää. Lonkka on siinä määrin polvea vahvempi, että keskimääräisillä raajojen mittasuhteilla suurimmat raudat kyykyssä saa ylös low-bar kyykyllä. Etukyykky vaatii reisiltä enemmän, lonkkanivelen jäädessä alikuormitukselle.

Ahaa. Eli kannattaa pitäytyä takakyykyssä.

Tjaa… Sopivin variaatio riippuu toki omista tavoitteista ja rajoitteista. Etukyykky aktivoi hyvin vartalon tukilihaksia, mutta voi olla vaikea jos raajojen mittasuhteet ovat epäsuotuisat tai ranteiden huono liikkuvuus tekee tangon pitämisen edessä hankalaksi. High bar on helpompi, mutta rasittaa alaselkää vähän kuten etukyykkykin. Low bar voi puolestaan olla hyvä jos polvet vihoittelevat tai nilkan liikkuvuus on huono — tai ehkä jos tavoitteena on suurimmat raudat.

Alkuperäiseen kysymykseesi liittyen, kuvan 4 henkilöllä polveen kohdistuva vääntömomentti on etukyykyssä $22\;\text{cm}/14\; \text{cm}=1{,}57$ low-bar -kyykyn vääntömomenttia suurempi. Mikäli kuvan 4 henkilöllä rajoittava tekijä olisi polveen kohdistuva vääntömomentti, niin hän saisi tällöin low-bar kyykyssä ylös $57$ % enemmän rautaa.

OK, ehkä kyykkyjen erot alkavat nyt hahmottua. Ja jokseenkin hahmotettavan mallin avulla.

Varoituksen sana kuitenkin siitä, että mallia ei kannata viedä liian pitkälle. Ensinnäkin, jokaisen ihmisen fysiologia on erilainen: luiden pituudet ovat erilaiset, lihakset kiinnittyvät luissa eri kohtiin ja luuston rakenne rajoittaa liikkuvuutta eri tavoin. Loppujen lopuksi kehokaan ei ole yksinkertainen vipujärjestelmä, jossa yksittäiset lihakset ovat vastuussa tietyn nivelen kierrosta, vaan se on luuston, lihasten, kalvojen ja jänteiden muodostama järjestelmä, joka toimii kokonaisuutena. Siten esimerkiksi kyykyssä aktiivisena ovat myös takareiden lihakset, vaikka niiden primääritehtävänä on polvinivelen taittaminen, ei ojentaminen. Iho siis kätkee sisäänsä paljon monimutkaisemmin toimivan kokonaisuuden kuin mitä yksinkertainen mekaniikka voi mallintaa.

Esimerkiksi jo penkkipunnerrusta on paljon vaikeampi ymmärtää yksinkertaisella mallilla. Siinä täytyisi ottaa huomioon lihasten voimakkuudet ja kiinnittymiskohdat olkaluuhun; jo olkanivel itsessään on huisan monimutkaisesti itseään stabiloiva pallonivel. 

Mutta tämä on sitä arjen fysiikkaa, josta oli aiemmin puhetta. Otetaan yksinkertaisin malli, jotta ymmärretään systeemistä olennaisin. 

Juuri noin! Eikä yritetäkään käyttää mallia liian tarkkojen analyysien tekemiseen. Riittää, että malli auttaa ymmärtämään systeemistä oleellisen. Salilla ulkoisten painojen vääntömomenttien tarkastelulla pääsee jo aika pitkälle. Tällaiset mallit ovat arvokkaita, koska niiden tarjoamaa ymmärrystä voi soveltaa lennosta myös käytännössä.

Oheistarkasteluna voidaan ottaa vaikka maastaveto, joka kuormittaa ensisijaisesti lonkkaa ja takaketjun lihaksia. Maastavedossa näkee usein taipumuksen selän pyöristämiseen noston aikana. Tämä on ymmärrettävää, koska pyöristäminen pienentää levytangon painon vipuvartta ja siten vääntömomenttia lonkkanivelen suhteen (Kuva 5). Pyöristämisellä voi siten saada ylös enemmän rautaa — ja samalla aiheuttaa itselleen välilevyn pullistuman! Maastavedossa raudat tulisikin saada ylös pitämällä ylävartalo jäykkänä. Tai jättää raudat nostamatta.

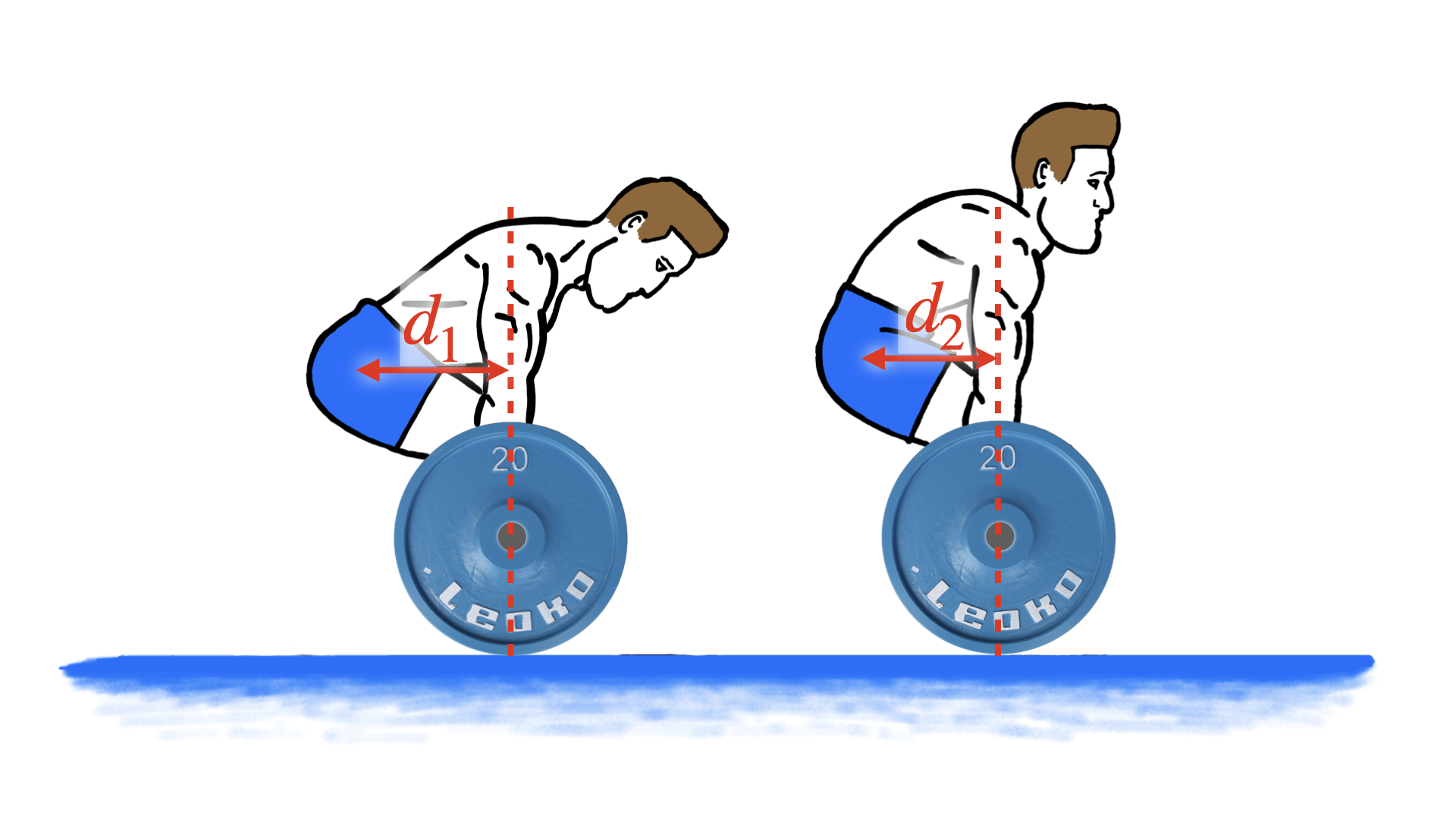
Kuva 5. Selän pyöristäminen maastanostossa pienentää levytangon painon vipuvartta ja siten vääntömomenttia lonkkanivelen suhteen ($d_1>d_2$).

Mutta myös salilaitteissa itsessään on kaikenlaista mekaniikkaa.

No tuo on totta. Ensimmäisenä mieleen tulee väkipyörät ja taljat, joita käytetään monissa laitteissa voiman suunnan muuttamiseen. Painopakat kulkevat pystysuunnassa ja voimaa halutaan kohdistaa johonkin toiseen suuntaan.

Siihen liittyen muuten kysymys: miksi ihmeessä joissakin laitteissa on liikkuva väkipyörä? Sehän ainoastaan puolittaa vaadittavan voiman. Eli jos liikkuvalla väkipyörällä nostaa 100 kg, niin se on ihan sama asia kuin nostaisi kiinteällä väkipyörällä 50 kg. Eli painoja pitää olla puolet enemmän.

Aika hyvä kysymys. Merkityksetön liikkuva väkipyörä ei ole, sillä taljoihin liittyy tässä suhteessa eräs juju. Tarkastellaanpa siis eroja laitteissa, joissa on kiinteä ja liikkuva väkipyörä. Tehdään tarkastelu lyhyellä videolla (Video 2).

Video 2. Kiinteän ja liikkuvan väkipyörän taljojen eroavaisuuden tarkastelua.

Yhteenvetona vielä, vaijerin jännitys eli henkilön kohdistama voima $T$ on 

• kiinteällä väkipyörällä $T=m(g+a_{vaijeri})$

• liikkuvalla väkipyörällä $T=(2m)(g+a_{vaijeri}/2)$ (massa on kaksinkertainen),

missä $a_{vaijeri}$ on vaijerin eli käden kiihtyvyys. Käden kohdistama voima kasvaa käden kiihtyessä suhteessa enemmän kiinteällä väkipyörällä kuin liikkuvalla väkipyörällä.

Ahaa! Eli arkisesti sanottuna, mitä enemmän liikettä, sitä tasaisempi kuormitus liikkuvalla väkipyörällä verrattuna kiinteään väkipyörään? Koska liikkeen määrä ja toistonopeudet myös tarkoittavat suuria kiihtyvyyksiä.

Niin, ja päinvastoin. Eli taljan tyypillä on sitä vähemmän merkitystä, mitä rauhallisemmin teet liikettä. Kiinteällä väkipyörällä suurempi voima liittyy massan suurempaan liike-energiaan, massan liikkuessa enemmän. Joissakin tilanteissa taljan tyyppi saattaa vaikuttaa myös kitkan merkitykseen.

Monet näistä asioista ovat intuitiivisesti tuttuja, mutta tällainen fysiikan analysointi auttaa kyllä selventämään ja perustelemaan näitä ilmiöitä.

Fysiikan tuntemus auttaa kuntosalilla hääräilevää harjoittelemaan tehokkaammin ja turvallisemmin. Vinkkinä, että esimerkiksi puhelimiin on saatavilla näppäriä sovelluksia, joiden avulla saa valmiiksi analysoituna levytangon nopeuksia ja kiihtyvyyksiä, pelkästään nostoja sivulta videoimalla. Näin fysiikka-analyysin saa osaksi treenaamista. Tai jos aihe kiinnostaa enemmän, kannattaa tutustua Jyväskylän avoimen yliopiston tarjoamaan kurssiin Kehosta mitattava hyvinvointitieto.